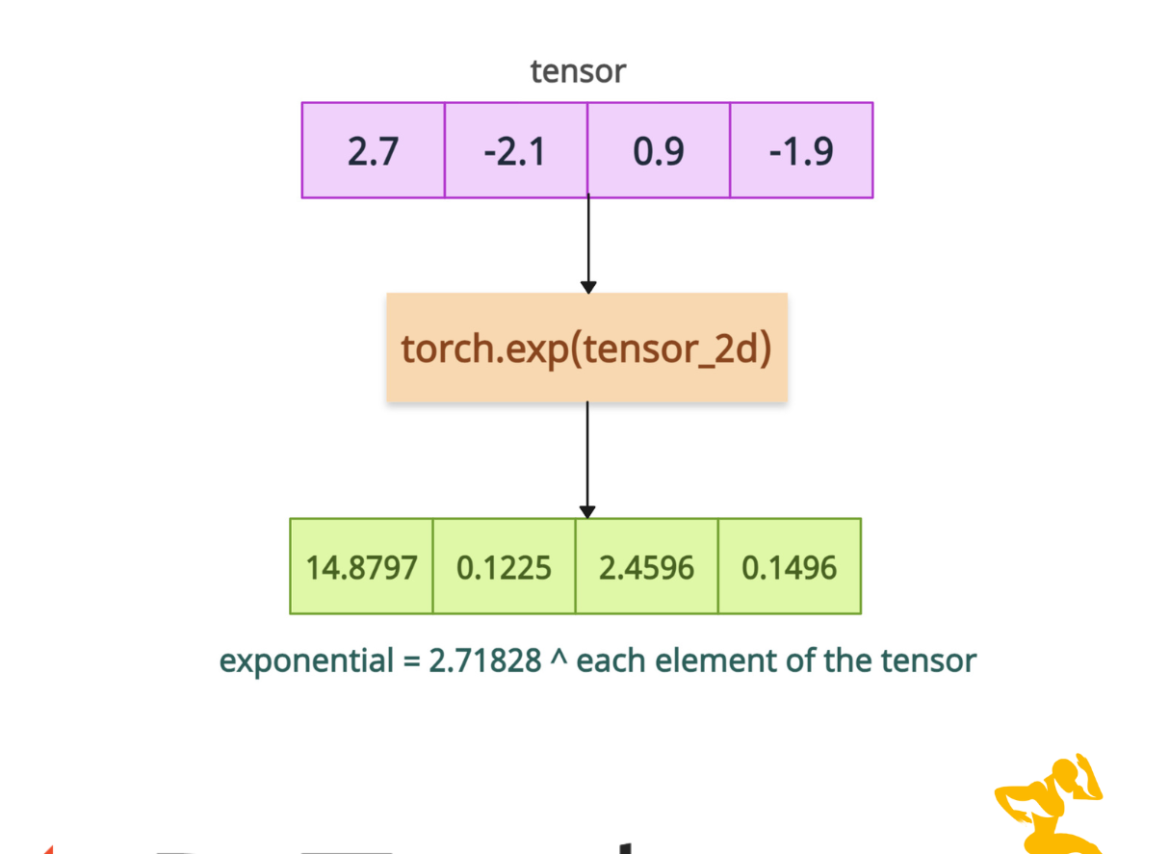
The torch.exp() method calculates the element-wise exponential of the input tensor. For each element x, it returns e^x, where e is Euler’s number (base of natural logarithms). The Euler’s number is 2.7182818. So, basically it is 2.7182818^input.
The standard exponential formula is this: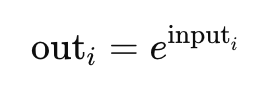
It is commonly used in activation functions, probability calculations, and mathematical modeling.
Syntax
torch.exp(input, out=None)
Parameters
| Argument | Description |
| input (Tensor) | It is an input tensor whose exponential values we need to calculate. |
| out (Tensor, optional) | It is an output tensor to store the result. It must match the shape and data type of the expected output. |
Basic element-wise exponential
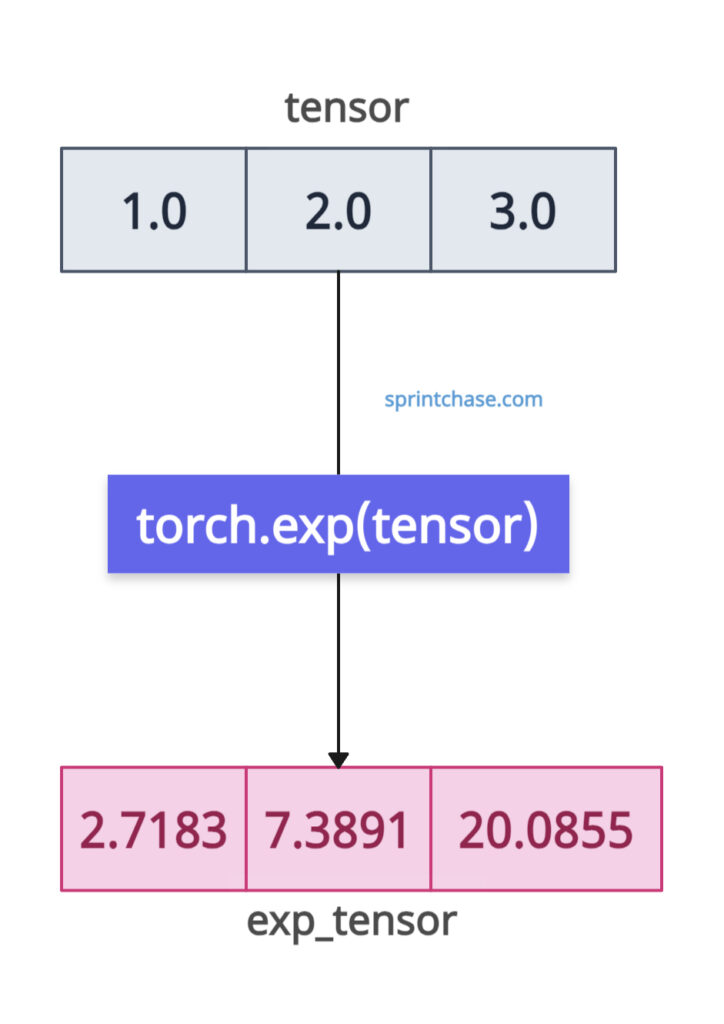
import torch # Input tensor tensor = torch.tensor([1.0, 2.0, 3.0]) exp_tensor = torch.exp(tensor) print(exp_tensor) # Output: tensor([ 2.7183, 7.3891, 20.0855])
In the above code, each tensor element is transformed as ( e^x ).
For ( x = [1.0, 2.0, 3.0] ), the result is ( [e^1.0, e^2.0, e^3.0] = [2.7183, 7.3891, 20.0855] ).
Matrix (2D Tensor)

import torch tensor_2d = torch.tensor([[1.0, 2.0], [3.0, 4.0]]) exp_2d = torch.exp(tensor_2d) print(tensor_2d) print(exp_2d) # Output: # tensor([[1., 2.], # [3., 4.]]) # tensor([[ 2.7183, 7.3891], # [20.0855, 54.5982]])
Using the “out” argument
If you have a pre-allocated tensor, you can use the “out” argument to store the result in this tensor and avoid creating a new tensor.
import torch # Input tensor tensor = torch.tensor([5.0, 6.0, 7.0]) # Pre-allocated output tensor out_tensor = torch.empty(3) torch.exp(tensor, out=out_tensor) print(out_tensor) # Output: tensor([ 148.4132, 403.4288, 1096.6332])
Complex input
The .exp() method handles the complex tensors very well.
import torch
import math
complex_tensor = torch.tensor([1j * math.pi], dtype=torch.complex64)
complex_exp = torch.exp(complex_tensor)
# Print the result
print("Input:", complex_tensor)
print("Exponential (e^{iπ}):", complex_exp)
# Output:
# Input: tensor([0.+3.1416j])
# Exponential (e^{iπ}): tensor([-1.-8.7423e-08j])
With Autograd (Backpropagation)
You can enable gradient computation while creating a tensor using the requires_grad=True argument and then calculate each element’s exponential.
import torch grad_tensor = torch.tensor([1.0, 2.0], requires_grad=True) grad_exp = torch.exp(grad_tensor) grad_exp.backward(torch.tensor([1.0, 1.0])) print(grad_tensor.grad) # Output: tensor([2.7183, 7.3891])
The above output illustrates the change in output when you adjust the inputs 1.0 and 2.0.
That’s all!