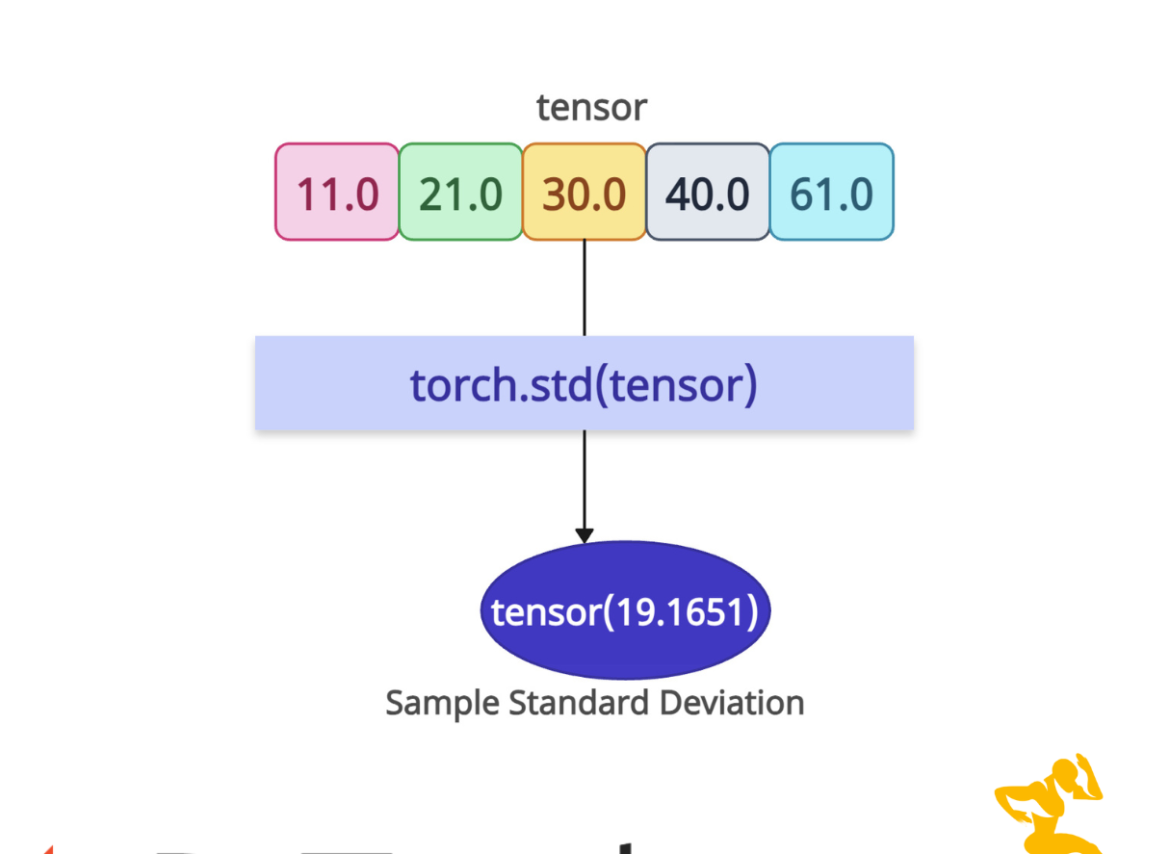
The torch.std() method calculates the standard deviation of elements in a tensor or along a specified dimension, measuring the dispersion of data around the mean.
But what is the standard deviation? The standard deviation is a measure of how spread out the values in a tensor are relative to its mean.
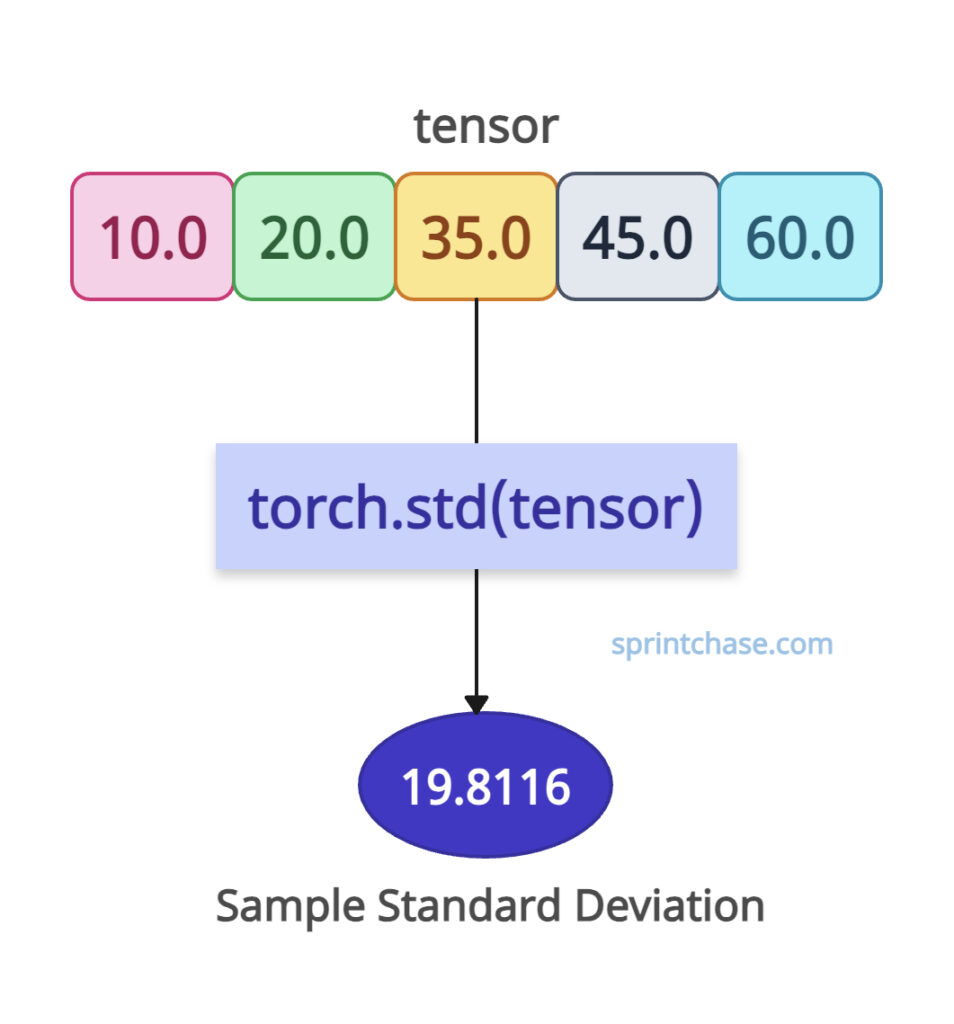
To calculate the sample standard deviation of all elements in a tensor, it should be unbiased and correction=1, which is the default setting. You don’t need to pass any extra arguments for that.
import torch tensor = torch.tensor([10.0, 20.0, 35.0, 45.0, 60.0]) # Standard deviation (unbiased, correction=1) std = torch.std(tensor) print(std) # Output: tensor(19.8116)
Syntax
torch.std(input,
dim=None,
correction=1,
keepdim=False,
out=None)
Parameters
| Argument | Description |
| input (Tensor) | It is an input tensor whose standard deviation you want to find. |
| dim (int, tuple of ints, or None, optional) | It is the dimension(s) along which to compute the standard deviation. |
| correction (int, optional) | It is the Bessel’s correction factor (degrees of freedom adjustment). The default is 1 (sample sd) (an unbiased estimate calculated by dividing by N-1). Set to 0 for population standard deviation (dividing by N). |
| keepdim (bool, optional) | If set to True, it retains the reduced dimensions with size 1. The default value is False. |
| out (Tensor, optional) | It is the output tensor to store the result. Default: None. |
Population vs. Sample Standard Deviation
The torch.std() method supports both population standard deviation (when unbiased=False) and sample standard deviation (default, unbiased=True).

The population standard deviation measures the spread of the entire population. For calculating population standard deviation, pass the correction = 0.
The sample standard deviation measures the spread of a subset (sample). Here, the correction = 1.
import torch tensor = torch.tensor([10.0, 20.0, 35.0, 45.0, 60.0]) # Population Standard deviation (correction=0) population_std = torch.std(tensor, correction=0) print(population_std) # Output: tensor(17.7200) # Standard deviation (correction=1) sample_std = torch.std(tensor) print(sample_std) # Output: tensor(19.8116)
When you have data for the whole group, use the population SD.
When you have a subset of the whole data, use the sample SD.
Along a specific dimension
For calculating row-wise standard deviation, pass dim=1.
For calculating column-wise standard deviation, pass the dim=0.
import torch
tensor = torch.tensor([[1.0, 22.0, 30.0],
[40.0, 5.0, 600.0]])
# Along rows (dim=1)
std_rows = torch.std(tensor, dim=1)
print(std_rows)
# Output: tensor([ 14.9778, 333.8787])
# Along columns (dim=0)
std_cols = torch.std(tensor, dim=0)
print(std_cols)
# Output: tensor([ 27.5772, 12.0208, 403.0509])
Row-wise Standard Deviation (dim=1):
-
Row 0: [1.0, 22.0, 30.0]
-
Mean = (1 + 22 + 30) / 3 = 17.67
-
Sample variance = [(1−17.67)² + (22−17.67)² + (30−17.67)²] / 2 = 224.33
-
Sample std = √224.33 ≈ 14.9778
-
-
Row 1: [40.0, 5.0, 600.0]
-
Mean = (40 + 5 + 600) / 3 = 215.0
-
Sample variance = [(40−215)² + (5−215)² + (600−215)²] / 2 = 111472.5
-
Sample std = √111472.5 ≈ 333.8787
-
Column-wise Standard Deviation (dim=0):
-
Column 0: [1.0, 40.0]
-
Mean = 20.5
-
Variance = [(1−20.5)² + (40−20.5)²] / 1 = 760.5
-
Std = √760.5 ≈ 27.5772
-
-
Column 1: [22.0, 5.0]
-
Mean = 13.5
-
Variance = 144.5
-
Std = √144.5 ≈ 12.0208
-
-
Column 2: [30.0, 600.0]
-
Mean = 315.0
-
Variance = 162444.0
-
Std = √162444 ≈ 403.0509
-
Using keepdim=True
It retains the reduced dimension as size 1.
import torch
tensor = torch.tensor([[1.0, 2.0, 3.0],
[4.0, 5.0, 6.0]])
# Along Rows with keepdim=True
std_rows = torch.std(tensor, dim=1, keepdim=True)
print(std_rows)
# Output: tensor([[1.0000],
# [1.0000]])
In the above code, the keepdim=True argument preserves the dimension, resulting in a 2×1 tensor instead of a 1D tensor.
That’s all!