torch.remainder(): Element-wise Remainder of Division

The torch.remainder() method calculates element-wise remainder of division (modulo operation) following mathematical conventions, where the sign of the result matches the divisor. It aligns with Python’s % operator behavior.

The remainder is calculated as input – other * torch.div(input, other, rounding_mode=’trunc’), where the result has the same sign as other.

Here is the basic formula to calculate the remainder:

remainder = dividend - divisor * floor(dividend / divisor)

Syntax

torch.remainder(input, other, out=None)

Parameters

Argument	Description
input (Tensor, scalar)	It is the dividend tensor.
other (Tensor, scalar)	It is the divisor, either a tensor or a scalar value.
out (Tensor, optional)	It is the output tensor to store the result. If not provided, it defaults to None.

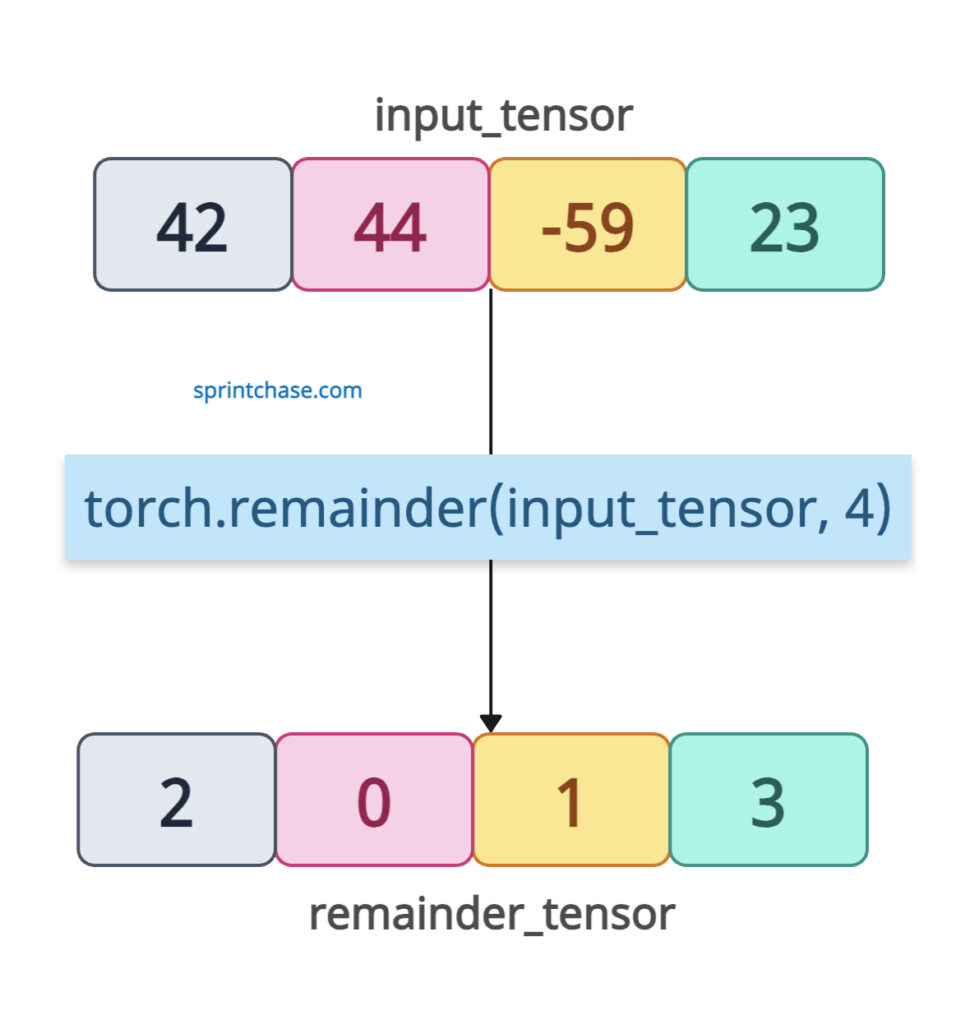
Scalar Division

It calculates remainders of a tensor divided by a scalar.

import torch

input_tensor = torch.tensor([42, 44, -59, 23])

remainder_tensor = torch.remainder(input_tensor, 4)

print(remainder_tensor)

# Output: tensor([2, 0, 1, 3])

In the above code, even for the negative number -59, this method returns a positive remainder (1), since it follows the sign of the divisor (4, which is positive).

The sign of the output tensor will match the divisor (4), which is positive, so that all remainders will be positive as well.

Tensor-to-Tensor Division

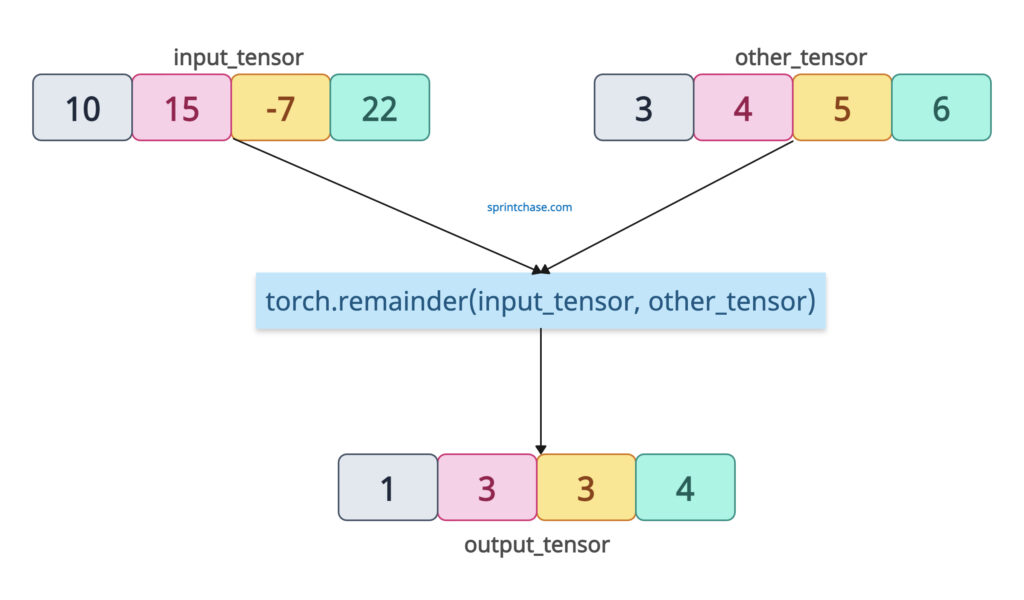
Let’s divide a tensor by another tensor, which gives us an element-wise remainder between two tensors.

import torch

input_tensor = torch.tensor([10, 15, -7, 22])

other_tensor = torch.tensor([3, 4, 5, 6])

output_tensor = torch.remainder(input_tensor, other_tensor)

print(output_tensor)

# Output: tensor([1, 3, 3, 4])

In the above code, each element of the input is divided by the corresponding element in the other. For -7 ÷ 5, the remainder is 3 because -7 = 5 * (-2) + 3.

Handling negative divisors

Let me demonstrate how the remainder’s sign follows the divisor.

import torch

input = torch.tensor([10, 20])

negative_divisor = torch.remainder(input, -3)

print(negative_divisor)  

# Output: tensor([-2, -1])

For 10 % -3:

10 / -3 = -3.33… → floor = -4

remainder = 10 – (-3 * -4) = 10 – 12 = -2

For 20 % -3:

20 / -3 = -6.66… → floor = -7

remainder = 20 – (-3 * -7) = 20 – 21 = -1

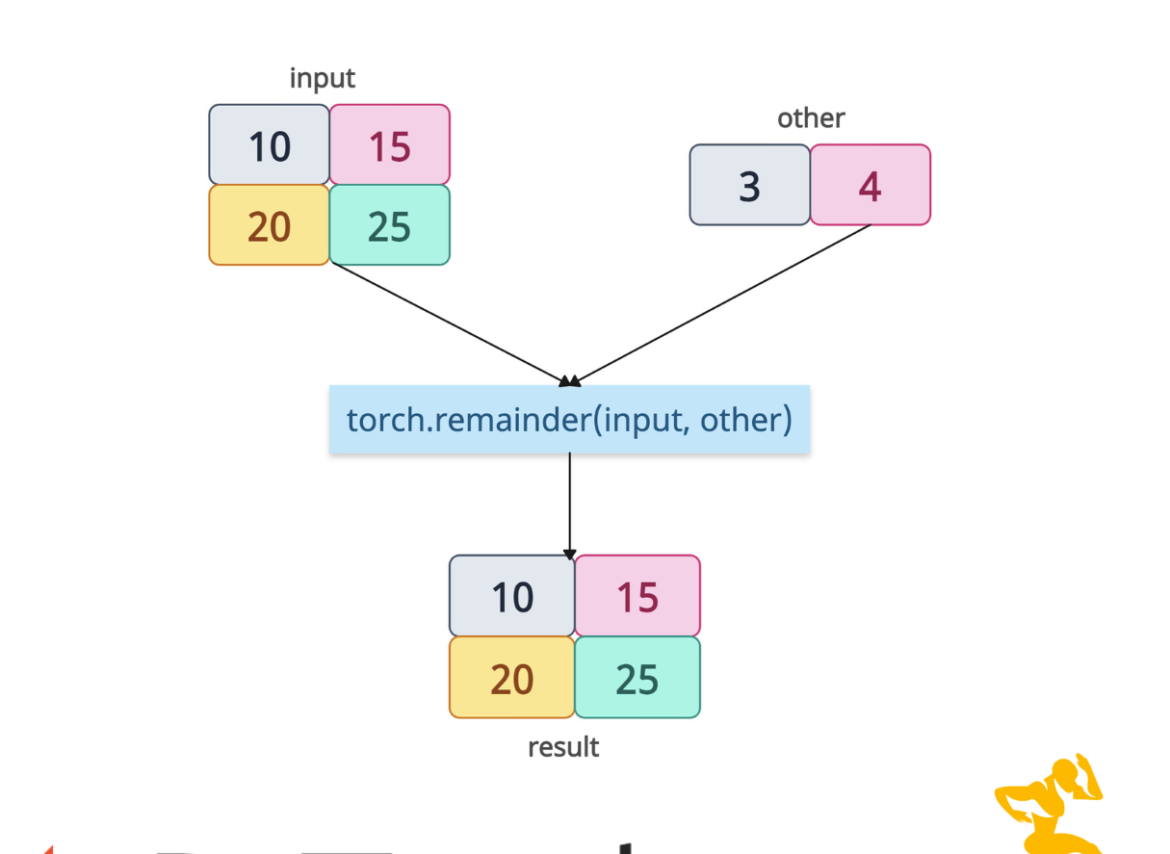
Broadcasting with Tensors

We can use broadcasting for tensors with different shapes.

import torch

input = torch.tensor([[10, 15], [20, 25]])

other = torch.tensor([3, 4])

result = torch.remainder(input, other)

print(result)

# Output:
# tensor([[1, 3],
#         [2, 1]])

In this code, the other is broadcast to match the input’s shape, calculating remainders element-wise.

That’s all!