torch.median(): Calculating a Median of Tensor Elements

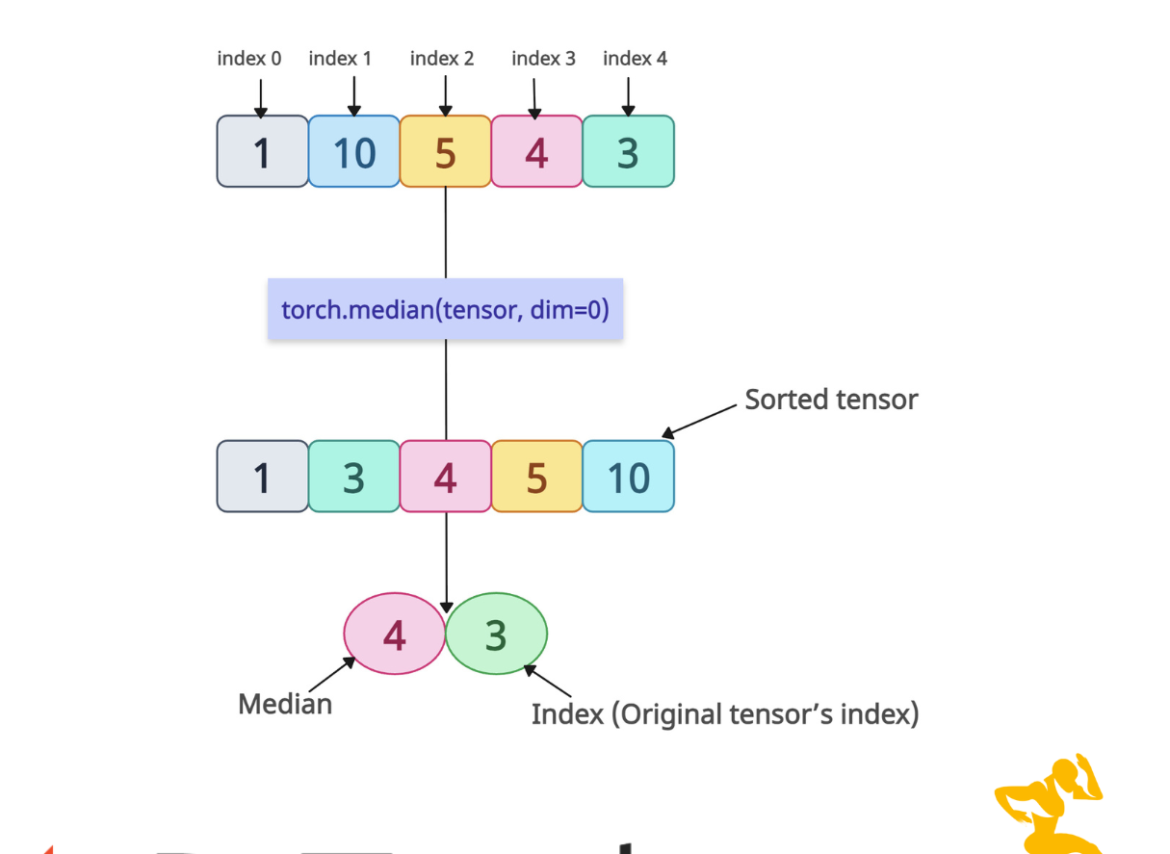
The torch.median() method calculates the median value of a tensor’s elements, either across all elements or along a specified dimension. The median value here is calculated by sorting the tensor’s elements and selecting the middle value.

It returns a tuple (median, index) where median is a scalar tensor with the median value, and index is the index of the median value in the original tensor.

When the number of elements is even, torch.median() does NOT average the two middle elements. Instead, it returns the lower of the two middle values (like numpy.median with method=’lower’). It does not calculate an actual statistical median when there’s an even number of elements.

If multiple elements equal the median, the method returns the index of the lowest value.

Syntax

torch.median(input, dim=-1, keepdim=False, out=None)

Parameters

Argument	Description
input (Tensor)	It is an input tensor.
dim (int, optional)	It is the dimension along which to calculate the median. The default is None; if it is None, it will calculate across all the elements.
keepdim (bool, optional)	If True, it retains the reduced dimension as size 1 in the output.
out (tuple, optional)	It is a tuple (values, indices) to store the median values and their corresponding indices.

Median of all elements

You can calculate the median of a flattened tensor. Also, pass the dim=1 for 1D tensor; otherwise, you will face this error: TypeError: iteration over a 0-d tensor.

import torch

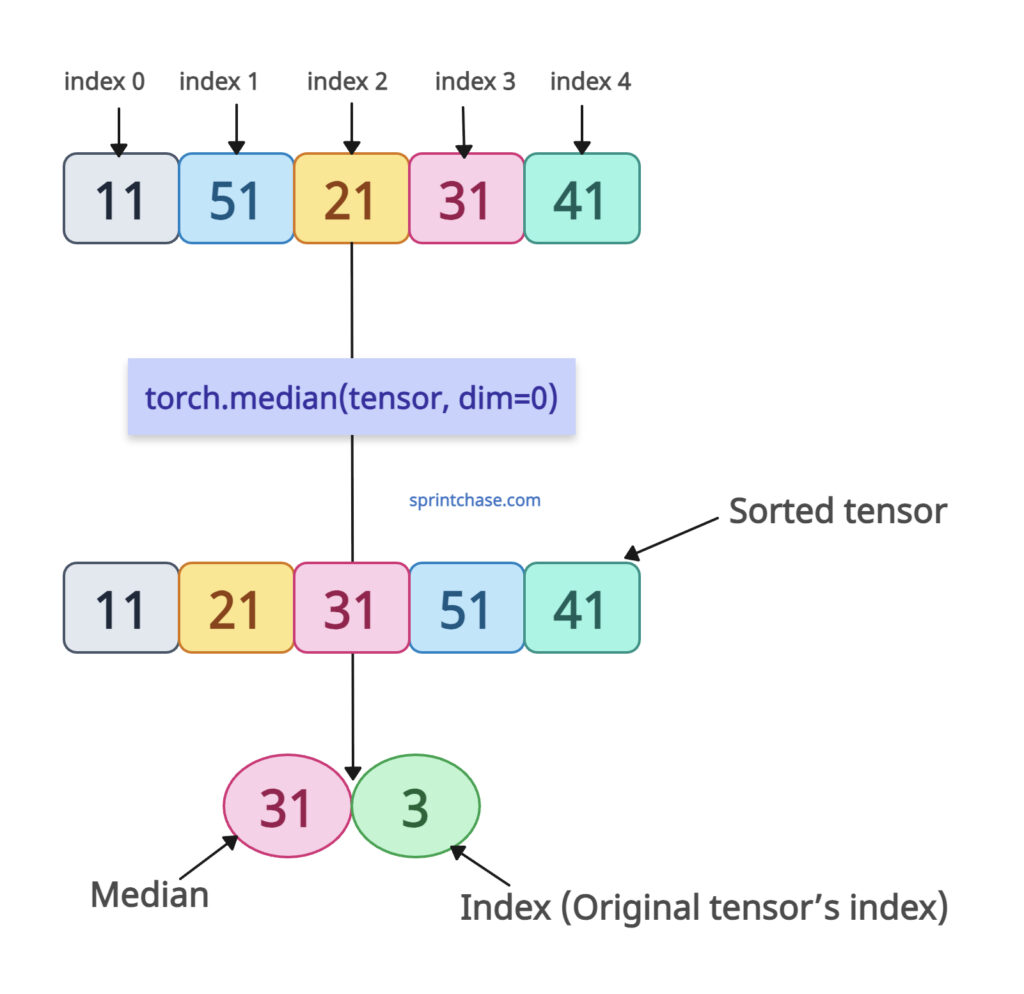
tensor = torch.tensor([11, 51, 21, 31, 41]) 

median, index = torch.median(tensor, dim=0)  # Specify dim=0

print(f"Median: {median}, Index: {index}")

# Output: Median: 31, Index: 3

First, the input tensor is sorted, which means the sorted tensor appears as follows: [11, 21, 31, 41, 51]. Then, the median is calculated.

Here, the median is 31, which is the middle value, and its index is 3 in the original tensor.

Median along a specific dimension

If you are working with a 2D tensor, you have two dimensions:

1. dim=0 → reduce along rows → operate column-wise
2. dim=1 → reduce along columns → operate row-wise

Based on your requirement, you can choose either dim=0 or dim=1.

Along rows

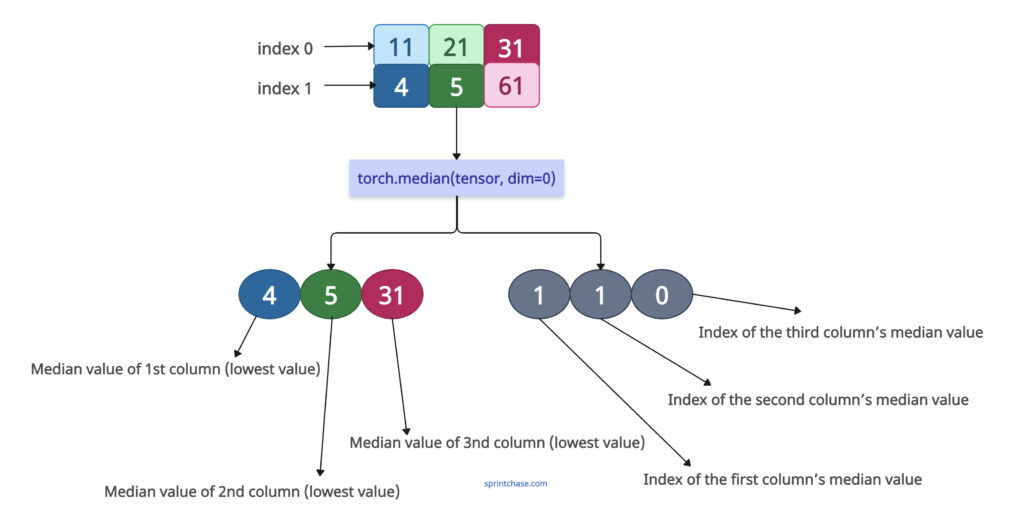Remember that we operate along rows, meaning we will operate column-wise.

import torch

tensor = torch.tensor([[11, 21, 31],
                      [4, 5, 61]])

values, indices = torch.median(tensor, dim=0)

print(f"Median values: {values}")
print(f"Indices: {indices}")

Median values: tensor([ 4, 5, 31])
Indices: tensor([1, 1, 0])

Here, the first column has two values: 11 and 4, and its median value is 4 because it is lower than 11, and its index is 1.

The second column has two values: 21 and 5, and its median value is 5, and its index is 1

The third column has two values: 31 and 61, and its median value is 31, and its index is 0.

Along columns

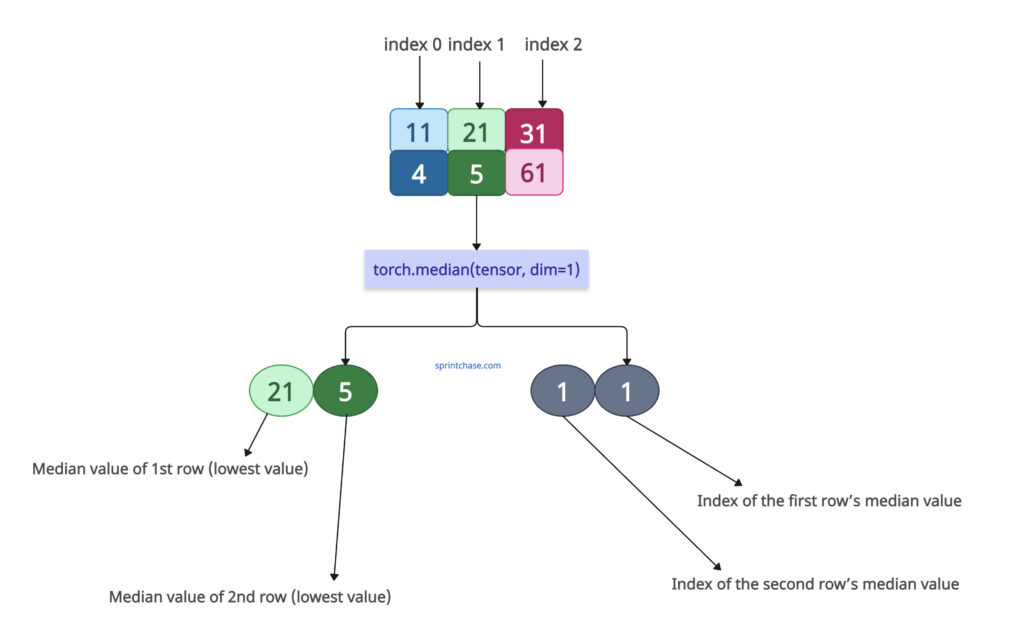Remember that we operate along columns, meaning we will operate row-wise.

import torch

tensor = torch.tensor([[11, 21, 31],
                      [4, 5, 61]])

values, indices = torch.median(tensor, dim=1)

print(f"Median values: {values}")
print(f"Indices: {indices}")

# Output: tensor([21,  5])
#         Indices: tensor([1, 1])

Here, the first row has three values: 11, 21, and 31, and its median is 21, and its index is 1.

The second column has three values: 4, 5, and 6, and its median is 5 and its index is 1.

Even-Sized Tensors

For even-sized tensors, the median is the lower value of the two middle values.

import torch

tensor = torch.tensor([11, 21, 31, 41])

median, index = torch.median(tensor, dim=0)

print(f"Median: {median}, Index: {index}")

# Output: Median: 21, Index: 1

You can see that Pytorch returns the lower value for integer tensors; it outputs 21 (index 1).

Empty Tensor

If you try to calculate the median of an empty tensor, it will raise an error.

import torch

tensor = torch.tensor([])
try:
    median, index = torch.median(tensor)
except TypeError as e:
    print(f"Error: {e}")

# Output: Error: iteration over a 0-d tensor

For floating-point tensors, the median is computed precisely; for integer tensors, it returns the lower middle value in even-sized cases.

That’s all!