torch.mean(): Calculating an Average of Tensor Elements

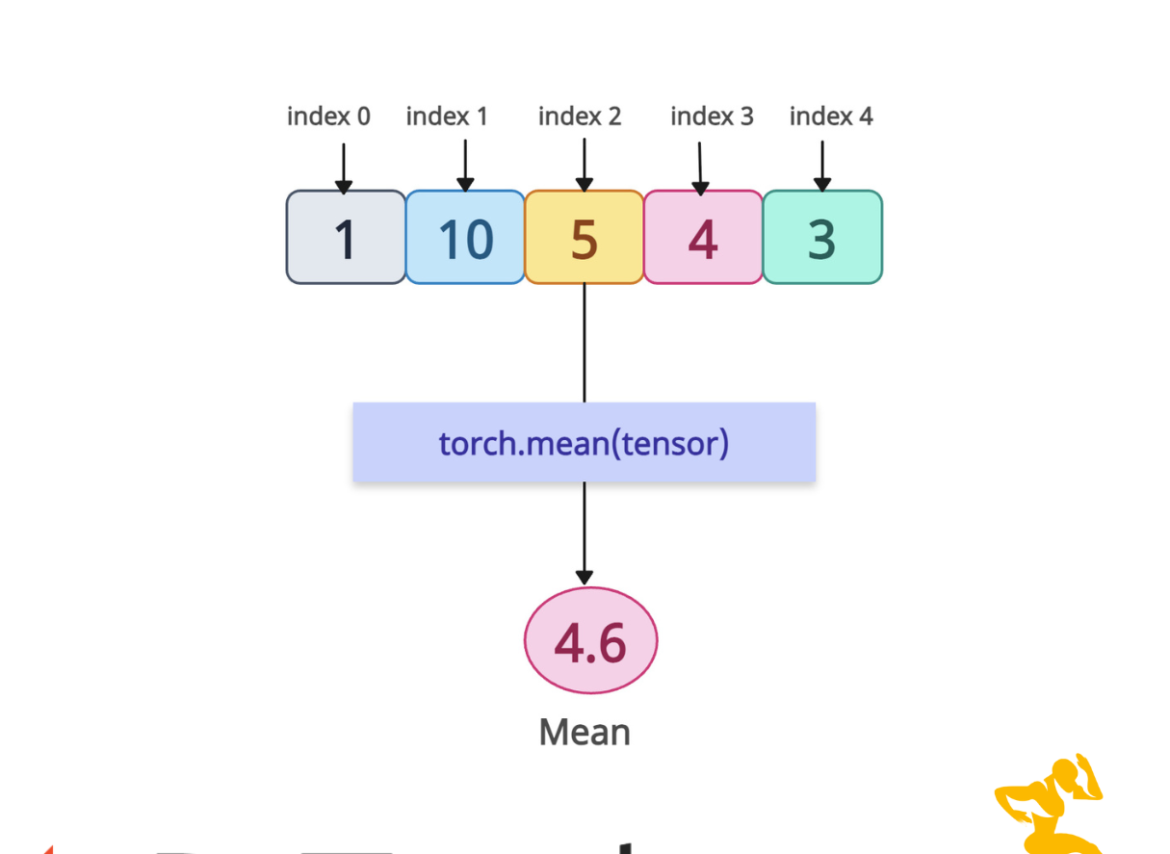
The torch.mean() method in PyTorch calculates the mean (average) of the tensor either along a specific dimension or across all the elements. It is a reduction operation since it reduces the number of elements in a tensor.

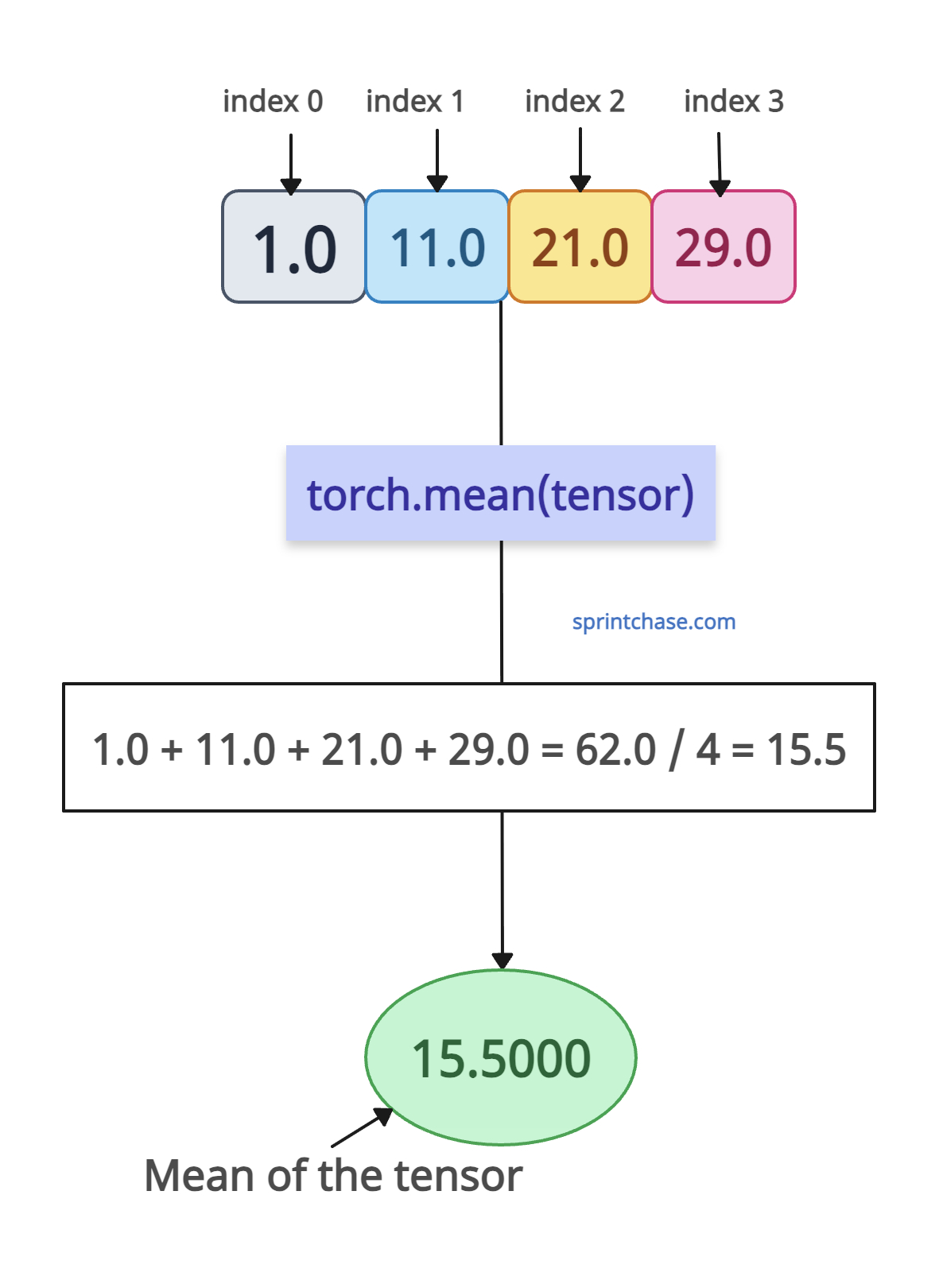To calculate the mean in mathematics, you sum all the elements and divide them by the number of elements.

Syntax

torch.mean(input, dim=None, keepdim=False, dtype=None, out=None)

Parameters

Argument	Description
input (Tensor)	It represents an input tensor whose mean you want to calculate.
dim (int or tuple of ints)	It is either a single dimension or a tuple of dimensions to reduce.
keepdim (bool)	If it is True, it retains the reduced dimension(s) with size 1. Default: False.
dtype (torch.dtype, optional)	It specifies the data type of the output tensor.
out (Tensor, optional)	It represents the output tensor. By default, it is None.

Mean of all elements

If you don’t pass any dimension to the function, by default, it will calculate the mean of all the elements in a tensor.

import torch

tensor = torch.tensor([1.0, 11.0, 21.0, 29.0])

# Mean of all elements: (1. + 11. + 21. + 29.) / 4
mean_of_all = torch.mean(tensor)

print(mean_of_all)

# Output: tensor(15.5000)

You can see from the output that it is a scalar tensor.

Mean along a specific dimension

If you are working with a 2D tensor, you have two dimensions:

1. dim=0 → reduce along rows → operate column-wise
2. dim=1 → reduce along columns → operate row-wise

Based on your requirement, you can choose either dim=0 or dim=1.

Along rows

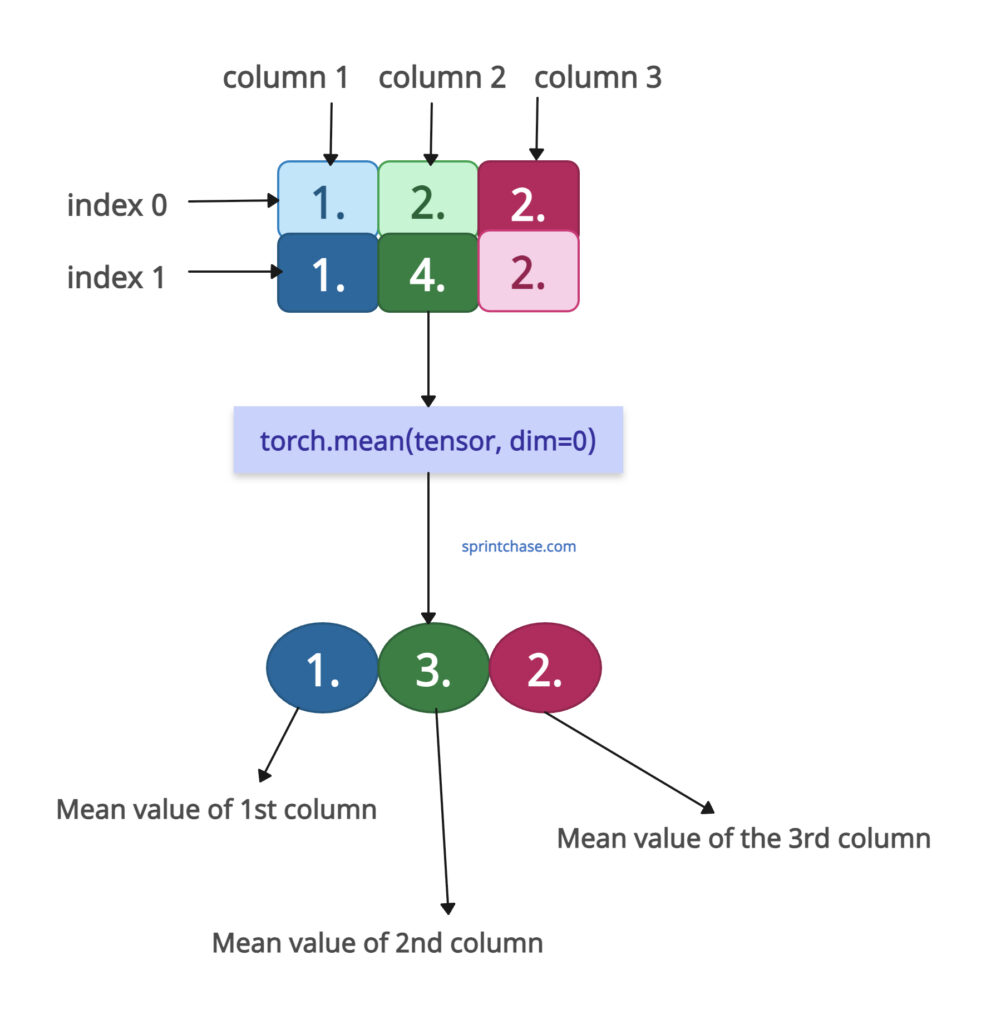Remember that operating along rows, meaning we will operate column-wise.

import torch

tensor = torch.tensor([[1., 2., 2.],
                       [1., 4., 2.]])

mean_across_rows = torch.mean(tensor, dim=0)

print(mean_across_rows)

# Output:
# tensor([1., 3., 2.])

Here, the first column has two values: 1. and 1., and its mean is also 1 because 1. + 1. = 2. / 2 = 1.

The second column has two values: 2. and 4., and its mean is 3 because 2. + 4. = 6. / 2 = 3.

The third column has two values: 2. and 2., and its mean is 2 because 2. + 2. = 4. / 2 = 2.

Along columns

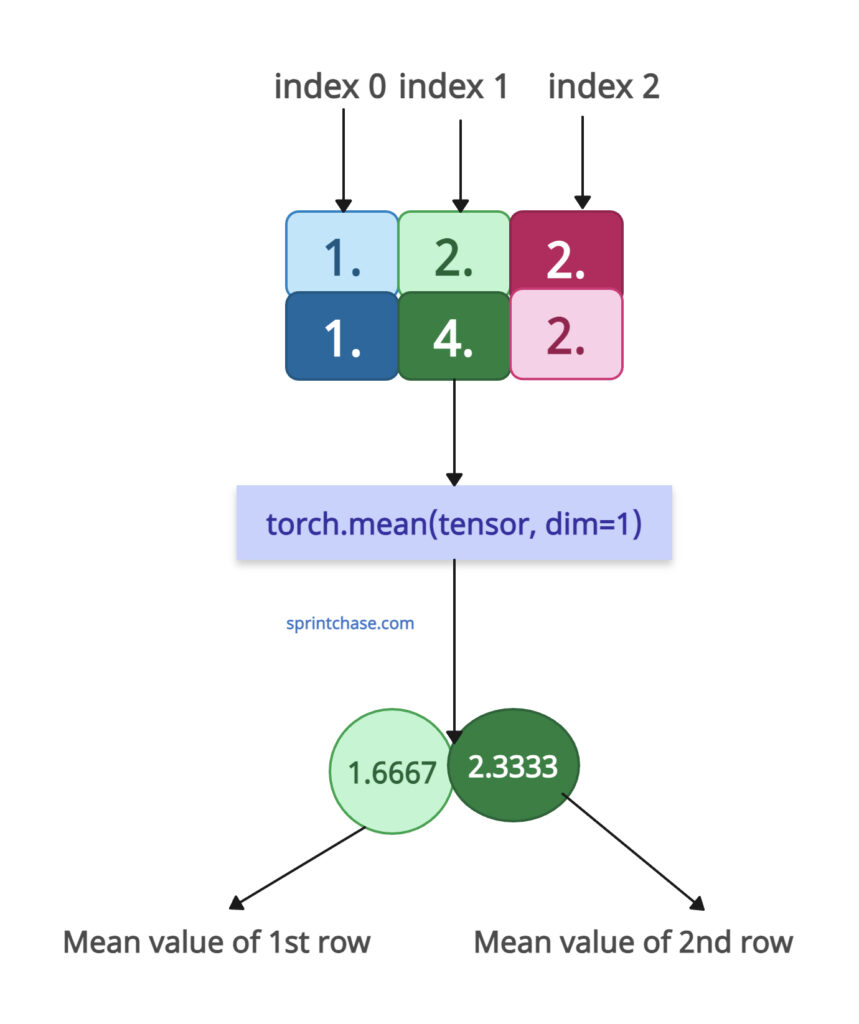Remember that operating along columns, meaning we will operate row-wise.

import torch

tensor = torch.tensor([[1., 2., 2.],
                       [1., 4., 2.]])

mean_across_columns = torch.mean(tensor, dim=1)

print(mean_across_columns)

# Output:
# tensor([1.6667, 2.3333])

Here, the first row has three values: 1., 2., and 2., and its mean is also 1.6667 because 1. + 2. + 2. = 5. / 3 = 1.6667.

The second column has three values: 1., 4., and 2., and its mean is 2.3333 because 1. + 4. + 2. = 7. / 3 = 2.333.

Multi-Dimensional tensors

Let’s define a 3D tensor with the shape (2 x 2 x 2).

First, we need to understand the dimensions of the 3D tensor.

In a 2x2x2 tensor:

• dim=0: outermost dimension → there are two matrices.

• dim=1: rows within each matrix.

• dim=2: columns within each matrix.

If we pass dim = (1, 2), for each 2×2 matrix, we will calculate the mean of all elements.

import torch

multi_tensor = torch.tensor([[[1., 2.], [3., 4.]], [[5., 6.], [7., 8.]]])

multi_tensor_mean = torch.mean(multi_tensor, dim=(1, 2))

print(multi_tensor_mean)

# Output:
# tensor([2.5000, 6.5000])

For the first matrix [[1, 2], [3, 4]], mean = (1+2+3+4)/4=10/4=2.5

For the second matrix [[5, 6], [7, 8]], mean = (5+6+7+8)/4=26/4=6.5

Retain reduced dimension with keepdim

We can keep the reduced dimension as size 1 by passing keepdim = True for compatibility in further operations.

import torch

tensor_2d = torch.tensor([[1., 2., 3.], [4., 5., 6.]])

tensor_with_dim = torch.mean(tensor_2d, dim=1, keepdim=True)

print(tensor_with_dim)

# Output:
# tensor([[2.],
#         [5.]])

You can see that keepdim=True preserves the reduced dimension as size 1, which helps maintain the tensor structure in neural network pipelines or for broadcasting.

That’s all!