The torch.log2() method calculates the logarithm to the base 2 of each element of the input tensor. It is the inverse operation of 2^x. It is particularly helpful when logarithmic scaling is required.
The return value is also a tensor, and it has the same shape and data type as the input.
Syntax
torch.log2(input, out=None)
Parameters
| Argument | Description |
| input (Tensor) | It represents an input tensor. |
| out (Tensor, optional) | It represents an output tensor. If you have a pre-allocated tensor, it would be conducive. If you don’t provide this argument, a new tensor will be created. |
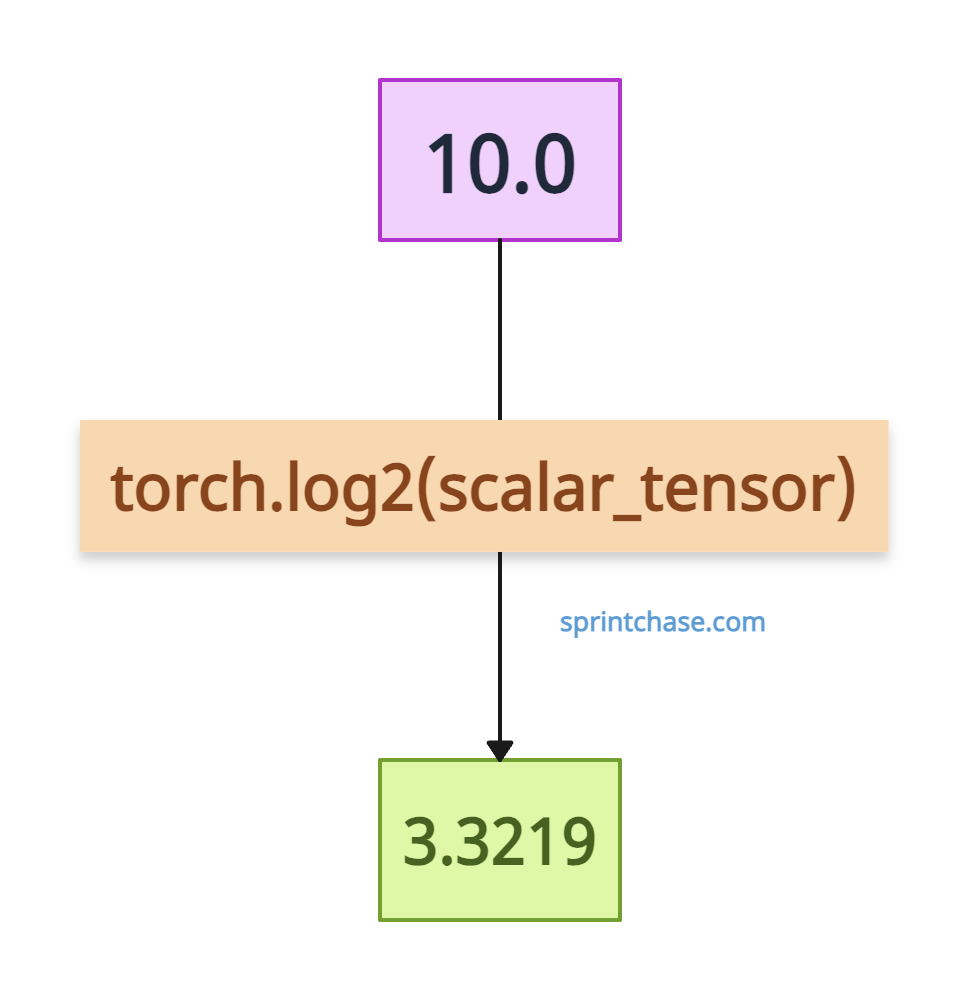
Calculating log2() of a scalar tensor
The scalar tensor only contains a single value. Let’s find out its log2().
import torch scalar_tensor = torch.tensor([10.0]) print(scalar_tensor) # Output: tensor([10.]) scalar_log2 = torch.log2(scalar_tensor) print(scalar_log2) # Output: tensor([3.3219])
1D tensor
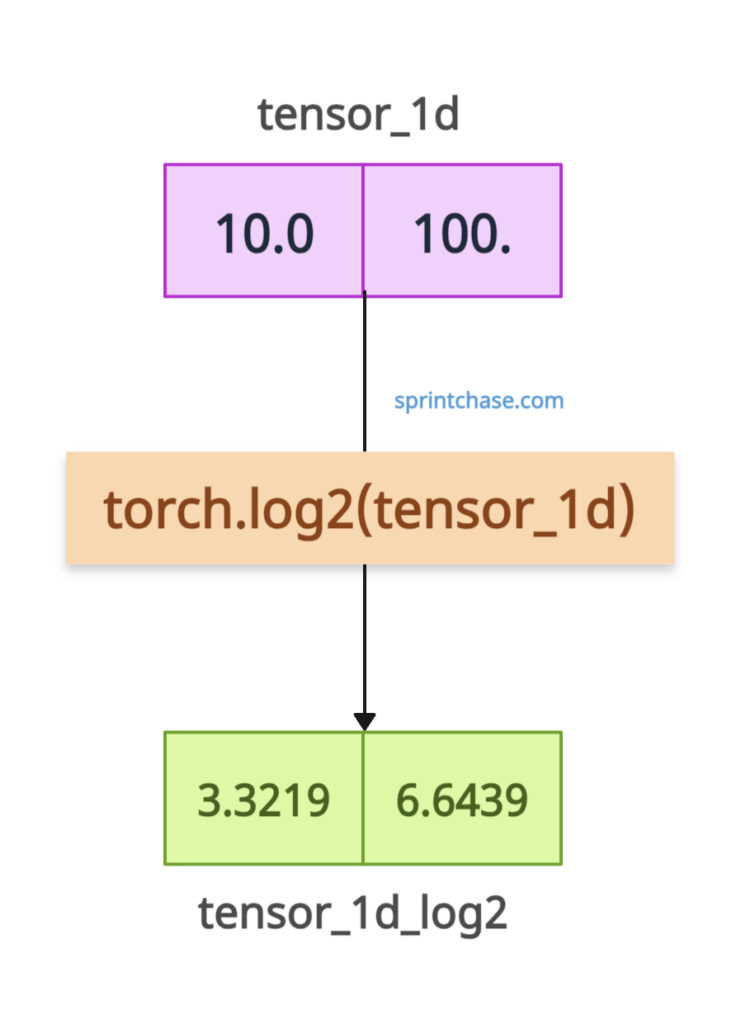
import torch tensor_1d = torch.tensor([10.0, 100.0]) print(tensor_1d) # Output: tensor([ 10., 100.]) tensor_1d_log2 = torch.log2(tensor_1d) print(tensor_1d_log2) # Output: tensor([3.3219, 6.6439])
2D tensor
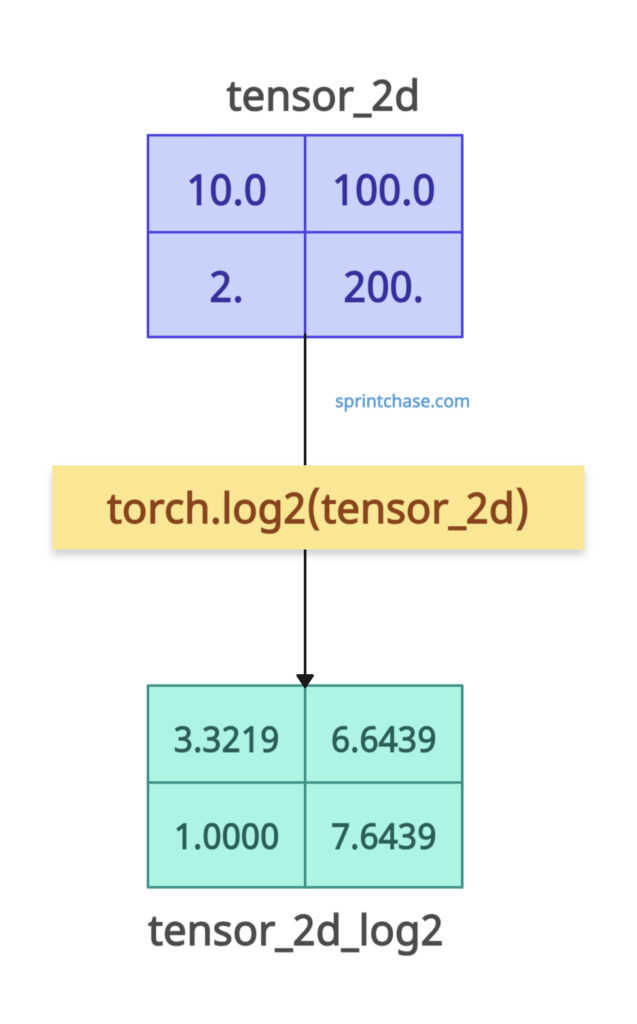
If the input tensor is 2D, the output tensor will also be 2D, with log2 values.
import torch tensor_2d = torch.tensor([[10.0, 100.0], [2.0, 200.0]]) print(tensor_2d) # # Output: tensor([[ 10., 100.], # [ 2., 200.]]) tensor_2d_log2 = torch.log2(tensor_2d) print(tensor_2d_log2) # Output: tensor([[3.3219, 6.6439], # [1.0000, 7.6439]])
In the above code, you can see that the operation is applied element-wise across the 2D tensor, preserving its shape.
Negative value and 0

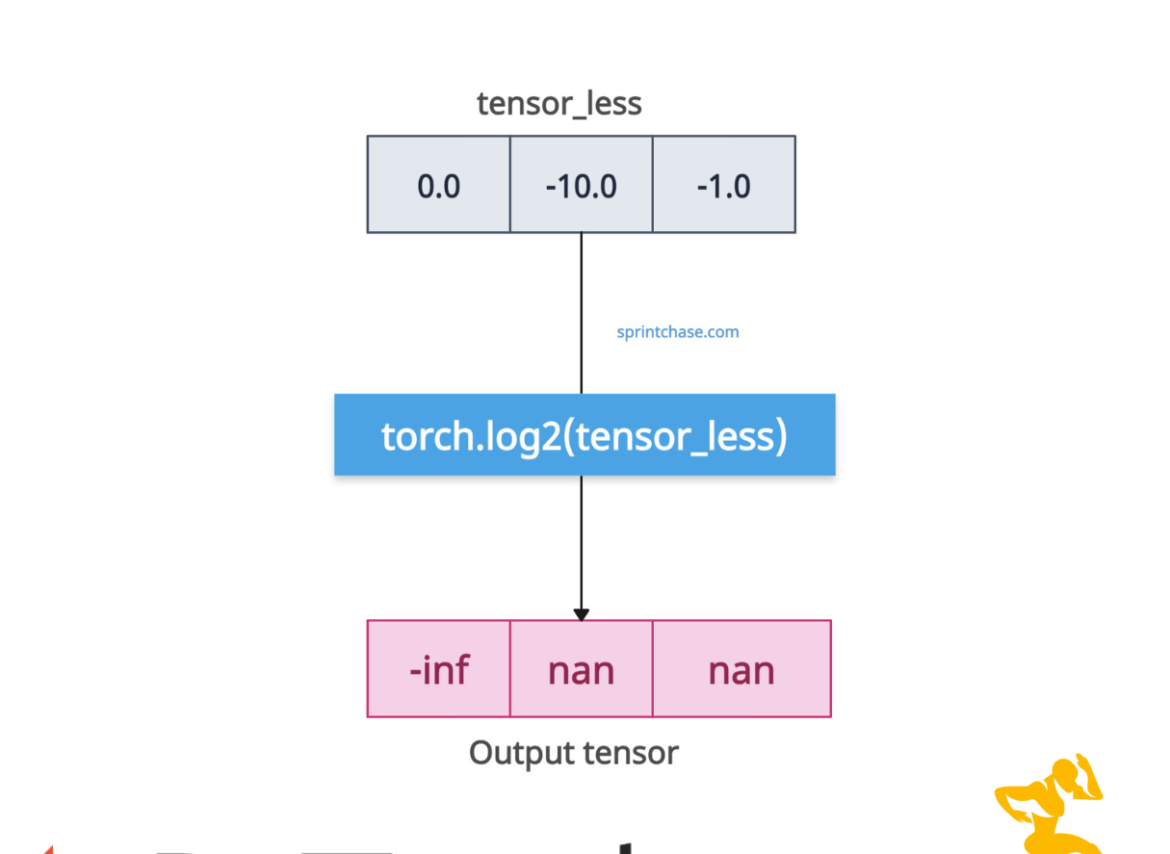
If you pass a non-negative input to the tensor, it will return nan.
If you pass 0, it will return -inf.import torch negative_zero_tensor = torch.tensor([-4.0, -1.0, -10.0, 0.0]) print(negative_zero_tensor) # Output: tensor([-4., -1., -10., 0.]) negative_zero_log2 = torch.log2(negative_zero_tensor) print(negative_zero_log2) # Output: tensor([nan, nan, nan, -inf])
Ensure that your inputs are positive to avoid nan values.
Complex numbers
If you pass the complex number, it will return a correct calculation and does not give NaN because it is acceptable to use the polar form.
import torch complex_tensor = torch.tensor([4+0j, 1j], dtype=torch.complex64) print(complex_tensor) # Output: tensor([4.+0.j, 0.+1.j]) complex_log2 = torch.log2(complex_tensor) print(complex_log2) # Output: tensor([2.+0.0000j, 0.+2.2662j])
Using the “out” argument
If you have a preallocated tensor, you can store the result of the log2() method in this tensor.import torch input_tensor = torch.tensor([1.0, 4.0, 16.0]) out = torch.empty(3) print(out) # Output: tensor([0., 0., 0.]) torch.log2(input_tensor, out=out) print(out) # Output: tensor([0., 2., 4.])
In the above code, we created an empty preallocated tensor using torch.empty() method and then store the log2 values into this tensor using the “out” parameter.
Plotting
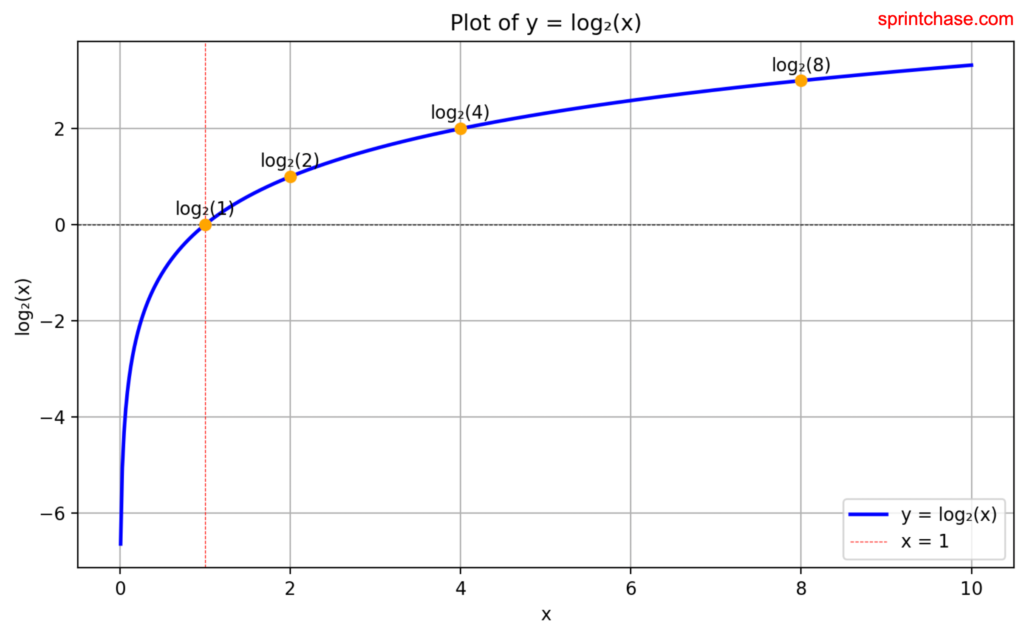
We can visually represent how the log2() method grows with increasing input values. For this, we need to have the matplotlib library, and if you haven’t already installed it, you can do so using the command below.pip install matplotlibNow, you can write the below code to plot a chart of the log2() method.
import torch
import matplotlib.pyplot as plt
# Create a range of x values > 0 (avoid log2(0) which is -inf)
x = torch.linspace(0.01, 10, steps=500)
y = torch.log2(x)
# Plot
plt.figure(figsize=(8, 5))
plt.plot(x.numpy(), y.numpy(), label='y = log₂(x)', color='blue', linewidth=2)
plt.axhline(0, color='black', linewidth=0.5, linestyle='--')
plt.axvline(1, color='red', linewidth=0.5, linestyle='--', label='x = 1')
# Annotate key points
plt.scatter([1, 2, 4, 8], [0, 1, 2, 3], color='orange', zorder=5)
for val in [1, 2, 4, 8]:
plt.text(val, torch.log2(torch.tensor(val)).item() +
0.2, f"log₂({val})", ha='center')
# Labels and title
plt.title("Plot of y = log₂(x)")
plt.xlabel("x")
plt.ylabel("log₂(x)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
 That’s all!
That’s all!