The torch.log() method in PyTorch calculates the natural logarithm of each element of the input tensor. It returns a tensor containing logarithmic values of the same shape and data type as the input.
It is a fundamental and one of the most used operations in machine learning, scientific computing, and statistics.
The mathematics formula is this: yi=loge(xi)
The .log() is different from the .log10() and .log2() methods because log10 calculates on base 10, and log2 calculates on base 2.
Syntax
torch.log(input, out=None)
Parameters
| Argument | Description |
| input (Tensor) | It is an input tensor whose log value we need to calculate. Make sure that it does not contain negative values. |
| out (Tensor, optional) | It is an output tensor to store the result. If you have a pre-allocated tensor, you can use that tensor to store the log results. |
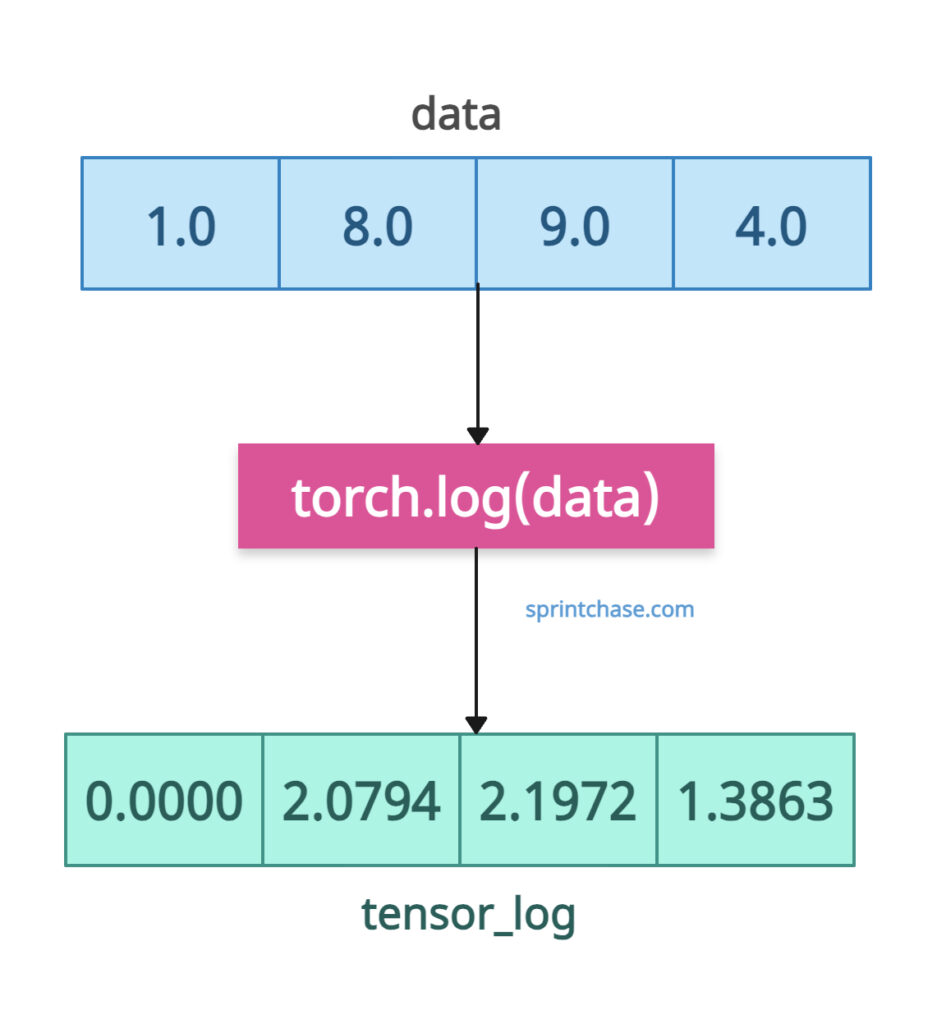
Natural log of 1D tensor
Let’s define a 1D tensor and find the log of it.
import torch data = torch.tensor([1.0, 8.0, 9.0, 4.0]) tensor_log = torch.log(data) print(tensor_log) # Output: tensor([0.0000, 2.0794, 2.1972, 1.3863])
The above output shows that each element of the input tensor “data” has been transformed into a logarithmic value. The returned tensor is a 1D tensor with the same shape and type.
2D Tensor (Matrix)
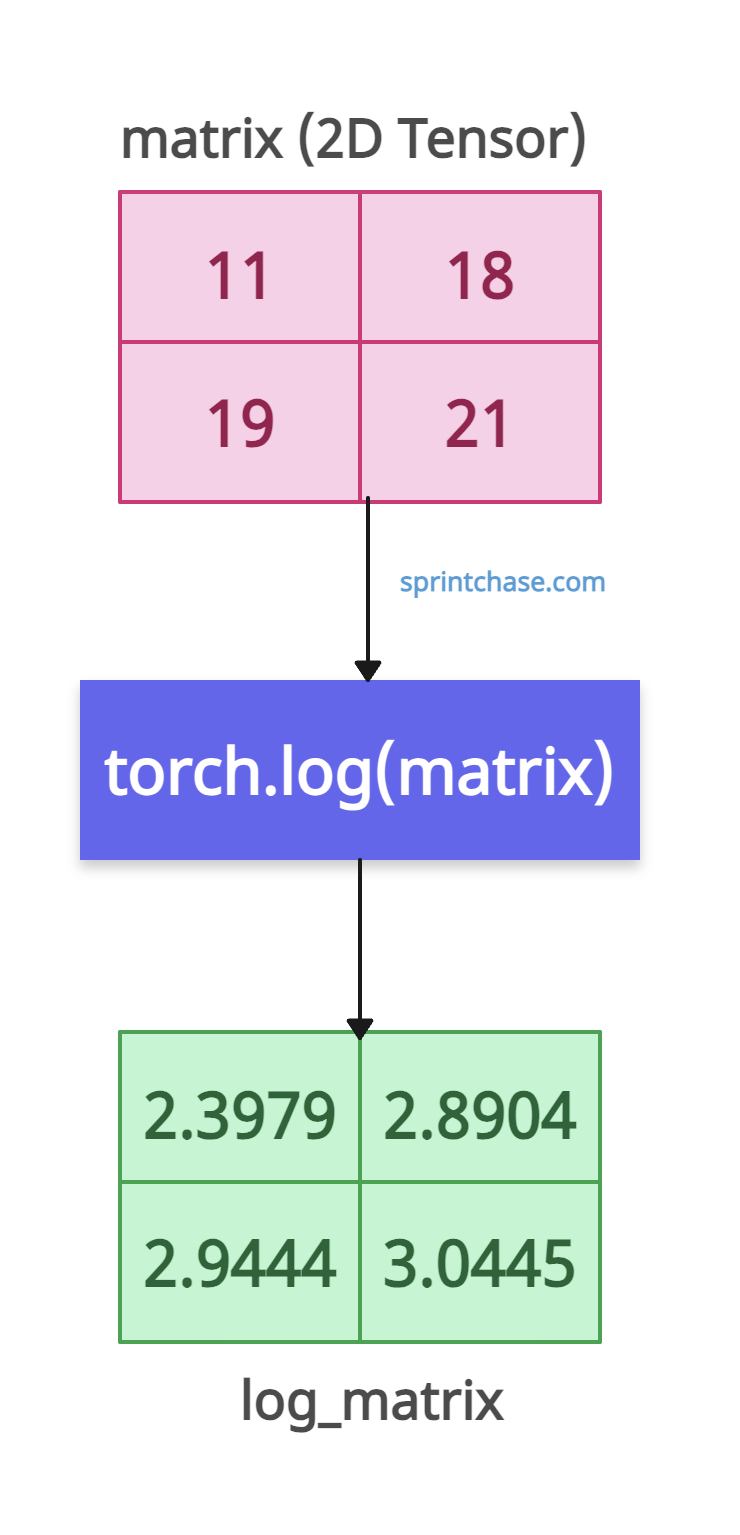
You can create a 2D tensor, a matrix containing rows and columns. Pass that matrix to the log() method, and it will return a 2D tensor containing the log value of each input element.
import torch matrix = torch.tensor([[11, 18], [19, 21]]) log_matrix = torch.log(matrix) print(log_matrix) # Output: tensor([[2.3979, 2.8904], # [2.9444, 3.0445]])
Zero or negative inputs
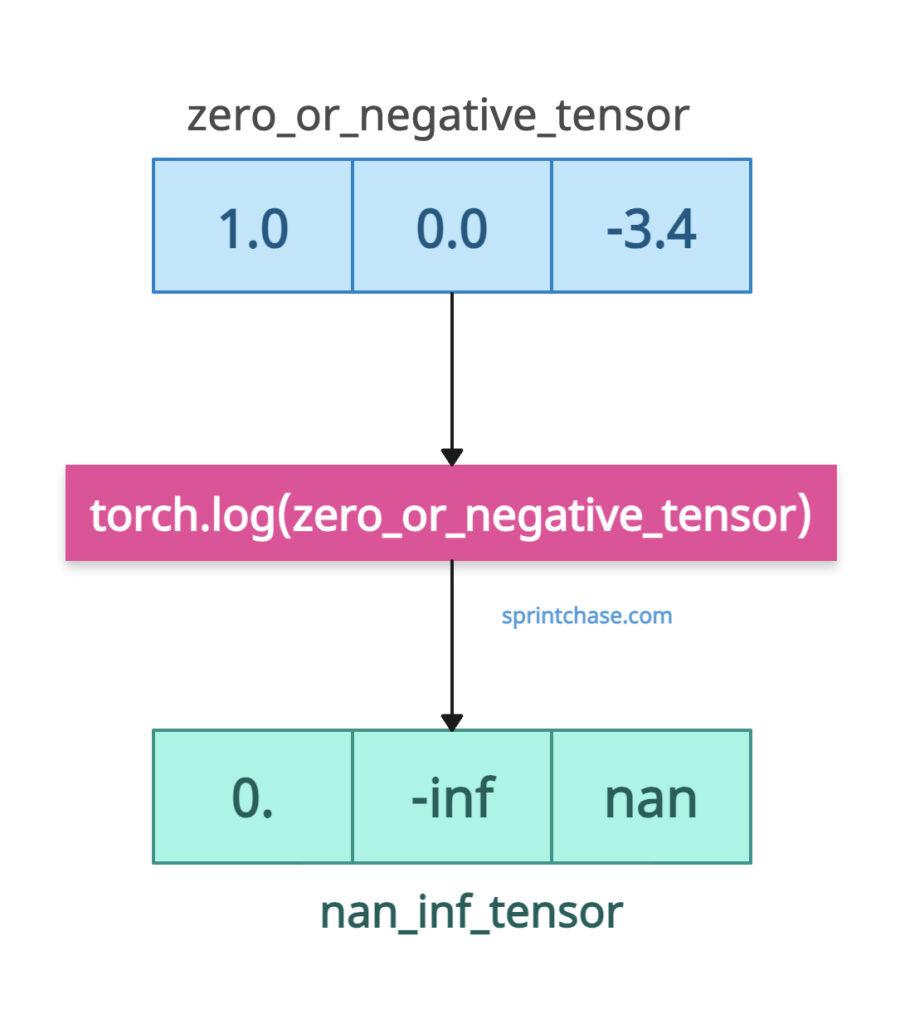
If you pass zero to the .log() function, it will return -inf. For a negative value, it will return nan.
import torch zero_or_negative_tensor = torch.tensor([1.0, 0.0, -3.4]) nan_inf_tensor = torch.log(zero_or_negative_tensor) print(nan_inf_tensor) # Output: tensor([0., -inf, nan])
Developers must include these edge cases while training the ML model.
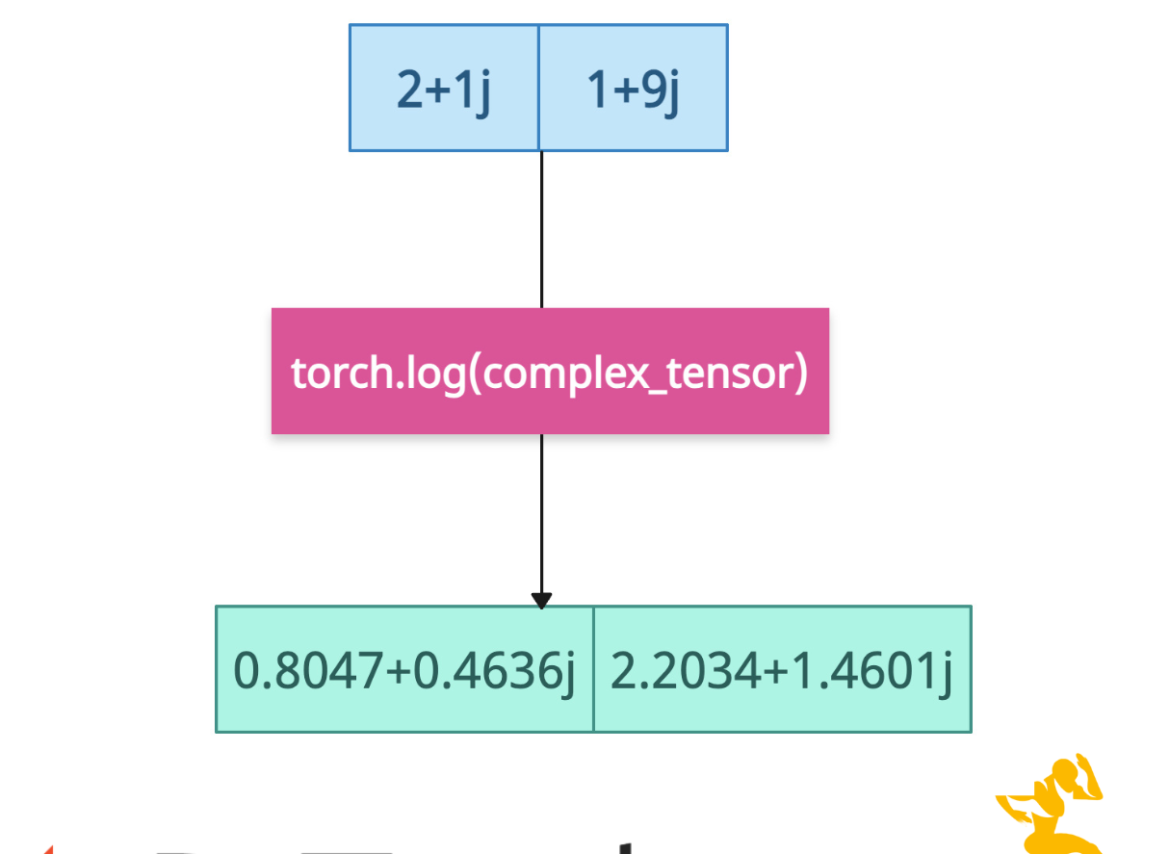
Complex numbers
For a complex tensor, the torch.log() method calculates the complex logarithm, where log(z) = log|z| + i*arg(z).
import torch complex_tensor = torch.tensor([2+1j, 1+9j], dtype=torch.complex64) complex_log = torch.log(complex_tensor) print(complex_log) # Output: tensor([0.8047+0.4636j, 2.2034+1.4601j])You can see from the above program that the output tensor is also a complex tensor containing log values.
Using the “out” argument
For in-place calculation, you can use the “out” argument. If you have a pre-allocated tensor using tensor.empty() or tensor.empty_like() function, you can store the result of log values in this tensor.
import torch tensor = torch.tensor([1.0, 2.0, 3.0]) pre_allocated_tensor = torch.empty(3) torch.log(tensor, out=pre_allocated_tensor) print(pre_allocated_tensor) # Output: tensor([0.0000, 0.6931, 1.0986])
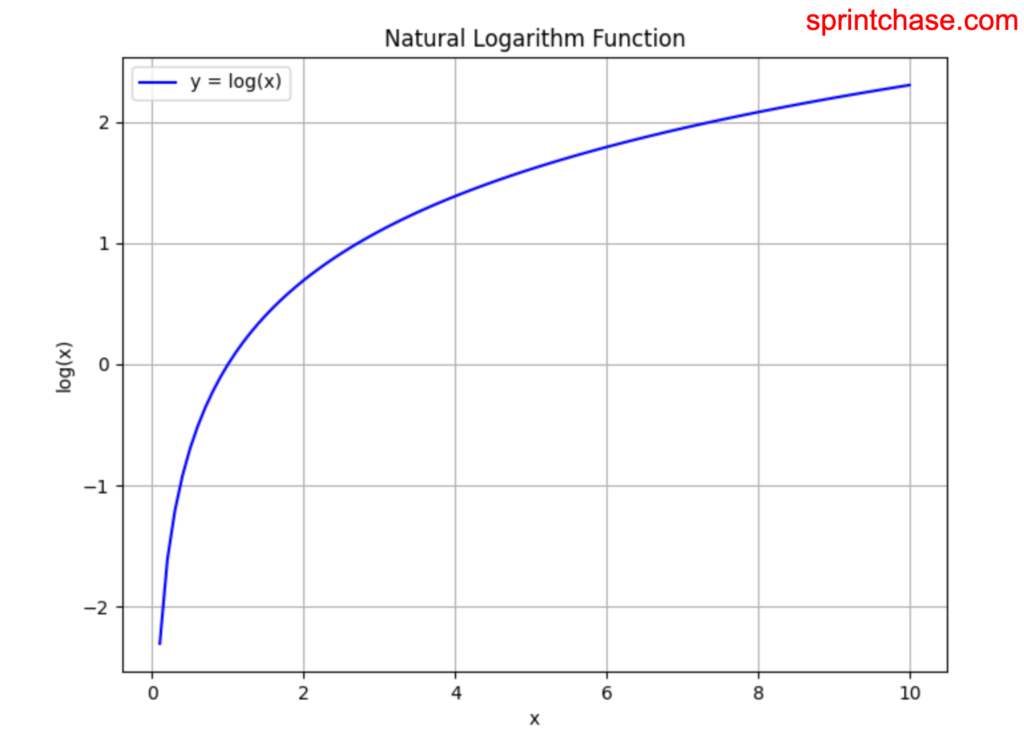
Plotting
To plot a chart of log values, we need the matplotlib library. We will create an evenly spaced tensor using torch.linspace() method.
import torch
import matplotlib.pyplot as plt
data = torch.linspace(0.1, 10.0, 100)
log_data = torch.log(data)
plt.figure(figsize=(8, 6))
plt.plot(data.numpy(), log_data.numpy(), 'b-', label='y = log(x)')
plt.title('Natural Logarithm Function')
plt.xlabel('x')
plt.ylabel('log(x)')
plt.grid(True)
plt.legend()
plt.savefig('log_plot.png')
plt.close()
print("Plot saved as 'log_plot.png'")
In the above code, we created a tensor, made a log of it, and then plotted the log points to the graph using various matplotlib methods.
Finally, saved the graph as a PNG to the current working directory. Its name is “log_plot.png” and it looks like this:
 That’s it!
That’s it!