torch.linspace(): Generating Evenly-Spaced 1D Tensor

The torch.linspace() method creates a one-dimensional tensor of size “steps” (provided by the user), evenly spaced elements between the inclusive start and end points.

Even spaced meaning values are spaced as (end – start) / (steps – 1). It uses 100 points if the “steps” argument is unspecified.

The use cases of the .linspace() function are for generating a sequence that requires uniform spacing, defining grid points, or interpolating values.

Function signature

torch.linspace(start, 
              end, 
              steps, 
              out=None, 
              dtype=None, 
              layout=torch.strided, 
              device=None, 
              requires_grad=False)

Parameters

Argument	Description
start (float or Tensor)	It specifies the starting value of the sequence. It is of type float or Tensor. If it is a Tensor, it must be a 1D tensor.
end (float or Tensor)	It specifies the ending value of the sequence, and it is inclusive. It can be of type float or Tensor. If Tensor, it must be a 1D tensor.
steps (int)	It is of type integer. It specifies the total number of points to generate between the start and ending points. It must be a positive integer. You can define it as the size of the newly constructed tensor.
out (Tensor, optional)	If you have a pre-allocated tensor, you can store the newly constructed tensor in this pre-allocated tensor using the “out” argument.
dtype (torch.dtype, optional)	It defines the data type of the output tensor. By default, it is inferred from the inputs.
layout (torch.layout, optional)	It defines the layout of the output tensor. By default, it is torch.strided.
device (torch.device, optional)	The device can be “CPU” or “cuda”, depending on your environment configuration.
requires_grad (bool, optional)	By default, it is False, but if True, it tracks gradients and supports backpropagation.

Generating linearly spaced points

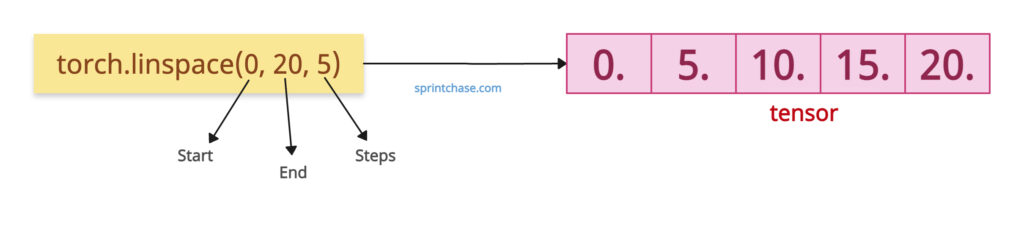
Let’s create five evenly spaced points from 0 to 20.

import torch

tensor = torch.linspace(0, 20, 5)

print(tensor)

# Output: tensor([ 0.,  5., 10., 15., 20.])

We can calculate the step size using this formula: (20 – 0) / (5 – 1) = 5. The tensor includes both start and end. The above output shows the step size = 5.

Single point edge case

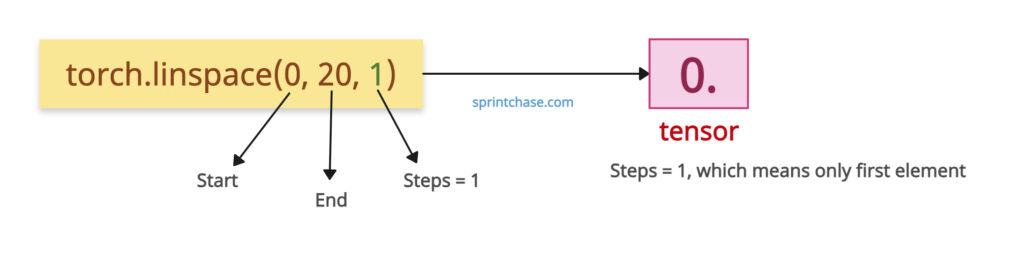
If you pass the steps = 1, it returns a tensor containing only the [start] point.

import torch

tensor = torch.linspace(0, 20, 1)

print(tensor)

# Output: tensor([ 0.])

The above output shows that it returns only the first element of the sequence because the step size is just 1.

What if steps = 0

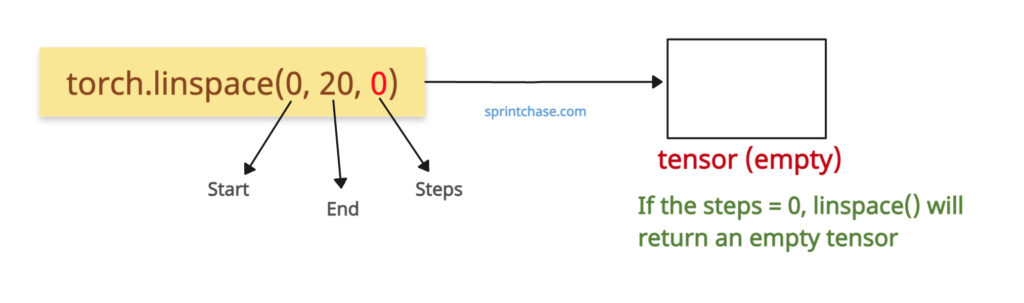
If you pass the steps = 0, it will return an empty tensor. It does not throw any RuntimeError now.

import torch

tensor = torch.linspace(0, 20, 0)

print(tensor)

# Output: tensor([])

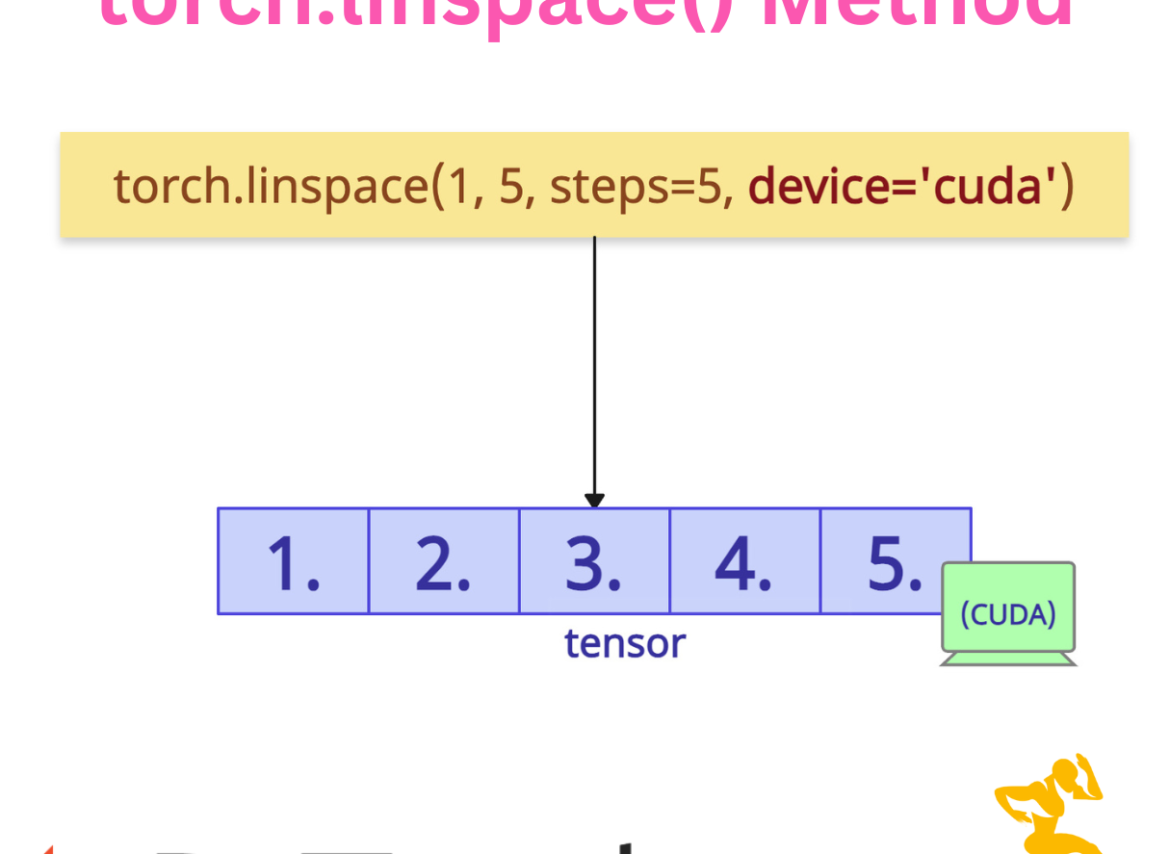
Specifying device

Let’s create a tensor on the GPU for faster computations by passing the “device” argument with a “cuda” value.

import torch

cuda_tensor = torch.linspace(1, 5, steps=5, device='cuda')

print(cuda_tensor)

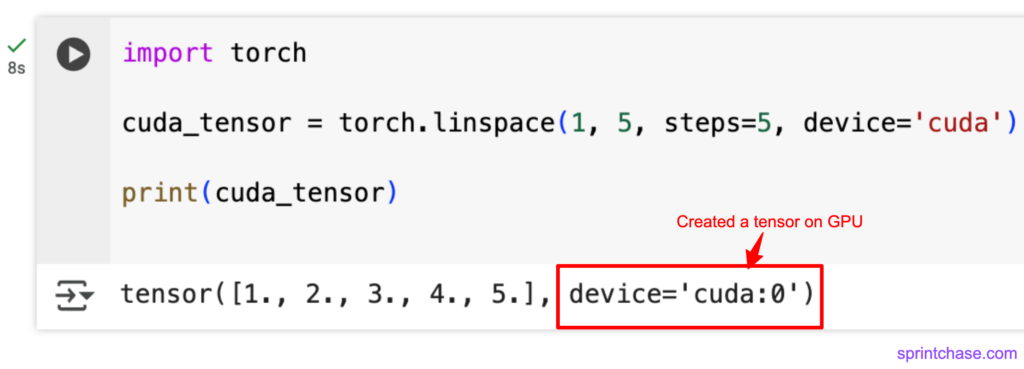
The above screenshot shows the proof that we can create a tensor on a GPU.

Specifying data type

Let’s generate 3 points from 1 to 5 with integer dtype.

import torch

tensor = torch.linspace(1, 5, 3, dtype=torch.int32)

print(tensor)

# Output: tensor([1, 3, 5], dtype=torch.int32)

You can see that the output tensor type is torch.int32.

Gradient Tracking

You can enable backpropagation by passing the “requires_grad=True” argument.

import torch

backpropagate_tensor = torch.linspace(1, 5, steps=5, device='cuda', requires_grad=True)

print(backpropagate_tensor)

 

Output to a pre-allocated Tensor

You can create a pre-allocated tensor using torch.empty() function and assign the value of the newly constructed evenly spaced tensor to this pre-defined tensor using the “out” argument.

import torch

pre_allocated_tensor = torch.empty(3)

torch.linspace(0, 3, steps=3, out=pre_allocated_tensor)

print(pre_allocated_tensor)

# Output: tensor([0.0000, 1.5000, 3.0000])

Comparison with torch.arange()

The torch.arange() method also generates a sequence of tensors, but it uses step size, not the number of points.

import torch

linspace_tensor = torch.linspace(0, 8, steps=5)
print(linspace_tensor)
# Output: tensor([0., 2., 4., 6., 8.])

arange_tensor = torch.arange(0, 10, 2)
print(arange_tensor)
# Output: tensor([0, 2, 4, 6, 8])

print(linspace_tensor.equal(arange_tensor))
# Output: True

Despite their different construction methods and default types, both tensors contain the same values and shape, so the .equal() returns True.

Plotting

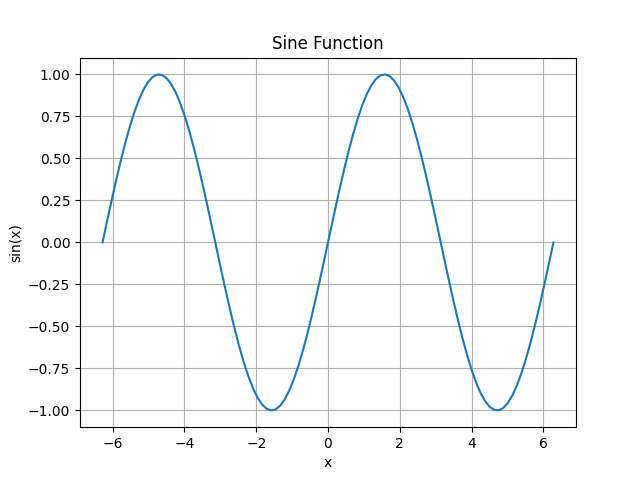
Let’s generate points for a sine plot and display the sine wave on the plot using the matplotlib library.

import torch
import matplotlib.pyplot as plt

x = torch.linspace(-2*torch.pi, 2*torch.pi, 100)
y = torch.sin(x)

plt.plot(x.numpy(), y.numpy())

plt.title("Sine Function")
plt.xlabel("x")
plt.ylabel("sin(x)")

plt.grid(True)

plt.savefig("sine_plot.png")

In your current working directory, one image has been saved called “sine_plot.png” that looks like the screenshot below:

That’s it!