torch.linalg.det() Method in PyTorch

The torch.linalg.det() method calculates the determinant of a square matrix. The determinant is a scalar value that provides important properties of a matrix, such as whether it is invertible (non-zero determinant) or singular (zero determinant).

This method is mainly used for checking matrix invertibility. It helps us analyze eigenvalues and matrix properties in machine learning and scientific computing.

For a 2×2 matrix [[a, b], [c, d]], the determinant is calculated as: ad – bc.

Syntax

torch.linalg.det(A, out=None)

Parameters

Argument	Description
A (Tensor)	It is a tensor of shape (*, n, n), where * is zero or more batch dimensions, and n is the size of the square matrix.
out (Tensor, optional)	It is the output tensor to store the result.

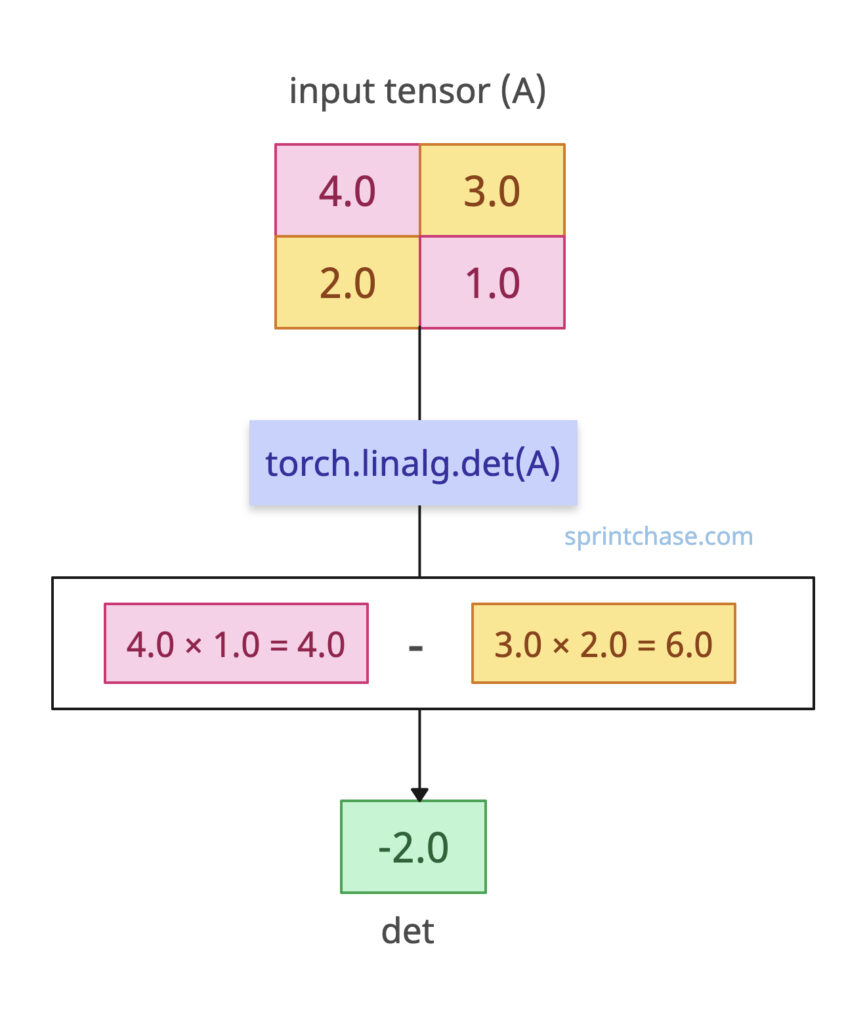
Determinant of a Single 2×2 Matrix

Let’s define a 2×2 tensor and find its determinant.

import torch

A = torch.tensor([[4.0, 3.0],
                  [2.0, 1.0]])

det = torch.linalg.det(A)

print(det)

# Output: tensor(-2.0)

You must be wondering why the output is tensor(-2.0). Let’s find out: Here, 4 × 1 – 3 × 2 = 4 – 6 = -2. A non-zero determinant indicates the matrix is invertible.

Identity Matrix

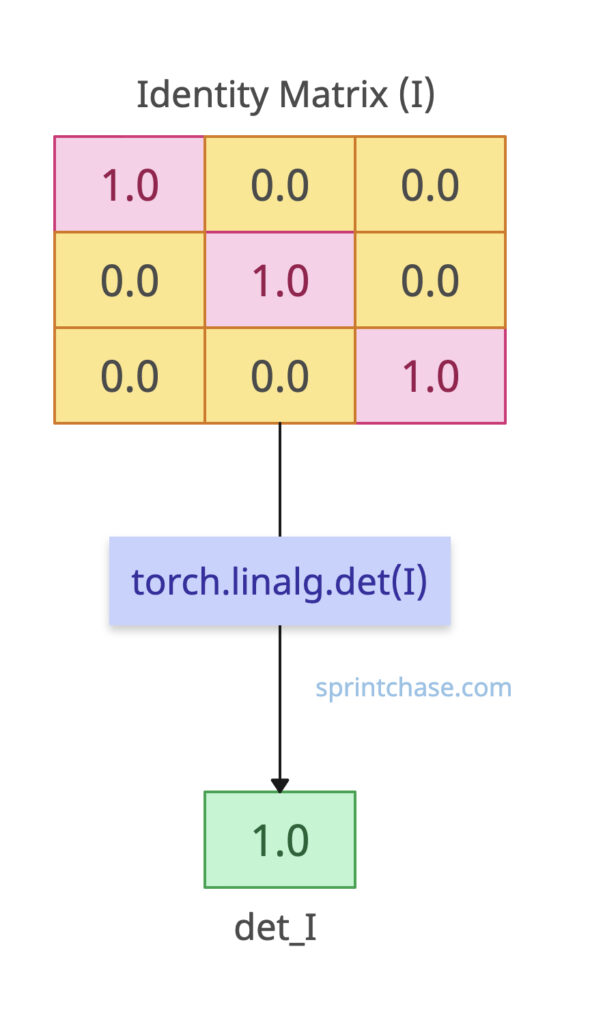What if the input is an identity matrix? Well, determinant of the Identity matrix is always 1. To create an identity matrix, use the torch.eye() method.

import torch

I = torch.eye(3)

det_I = torch.linalg.det(I)

print(det_I)

# Output: tensor(1.)

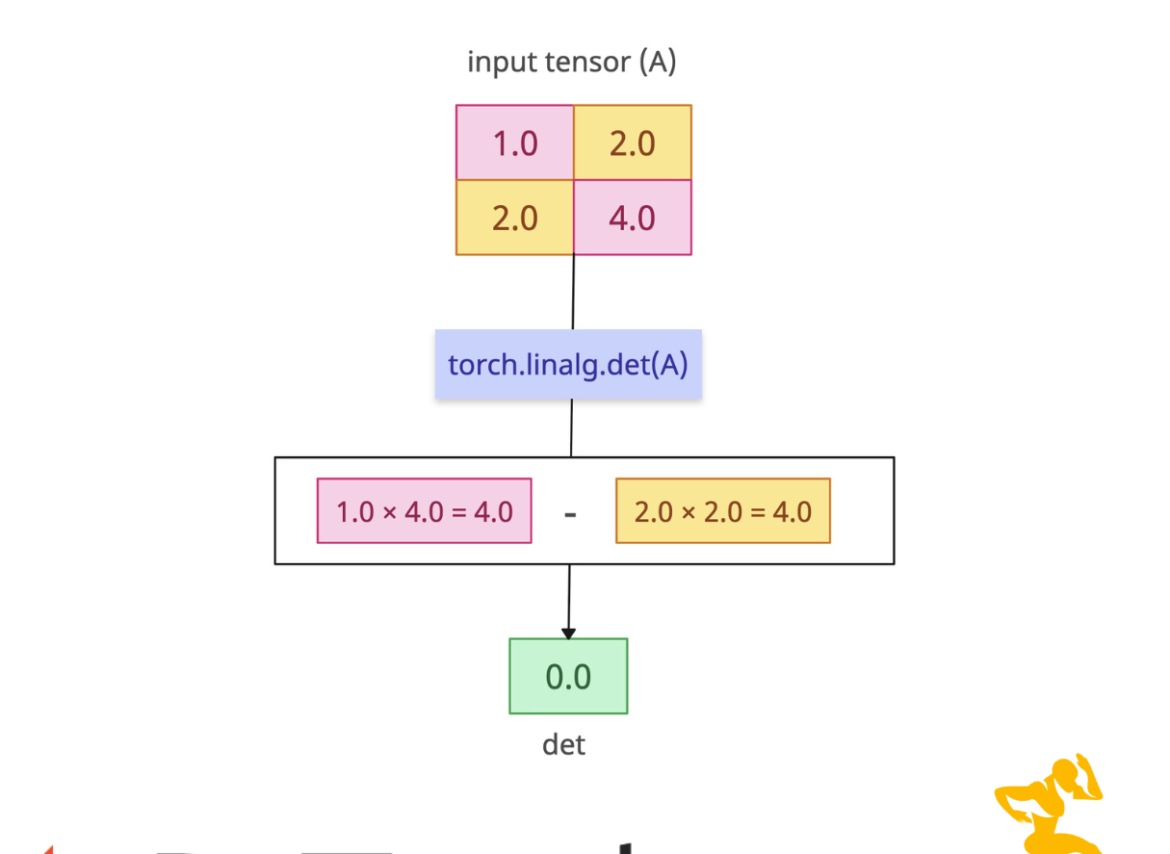
Singular Matrix (det=0)

If the input tensor is a singular matrix, the determinant is 0.

import torch

singular = torch.tensor([[1., 2.], [2., 4.]])

det = torch.linalg.det(singular)  # 1*4 - 2*2 = 0

print(det)

# Output: tensor(0.)

Complex Matrix

If the input is a complex matrix, the output is also a complex tensor.

import torch

complex_mat = torch.tensor([[1+2j, 3j], [4., 5-1j]])

det = torch.linalg.det(complex_mat)  # (1+2j)(5-1j) - (3j)(4)

print(det)

# Output: tensor(7.-3.j)

Empty matrix

If the input is an empty matrix, its determinant is 1.

import torch

empty_matrix = torch.empty(0, 0)

det = torch.linalg.det(empty_matrix)

print(det)

# Output: tensor(1.)

That’s all!