torch.dot: Multiplication of two 1D Tensors in PyTorch

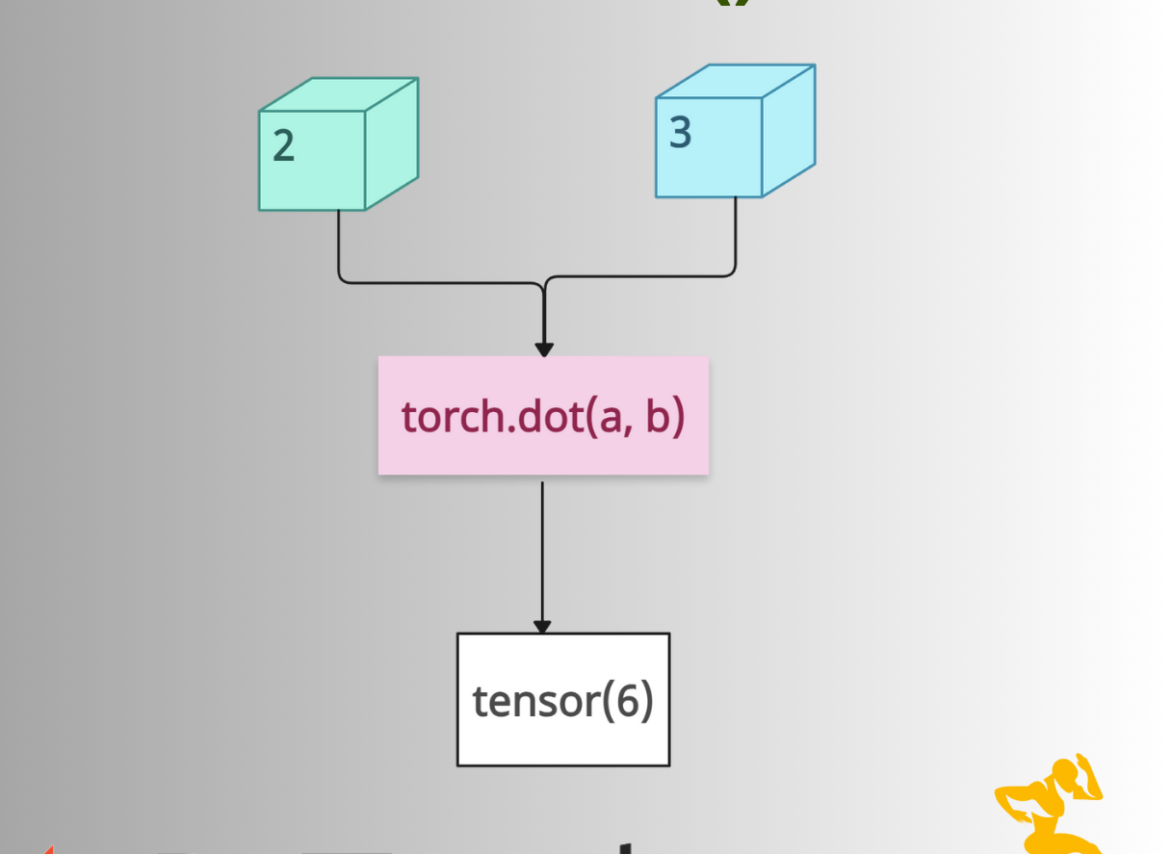
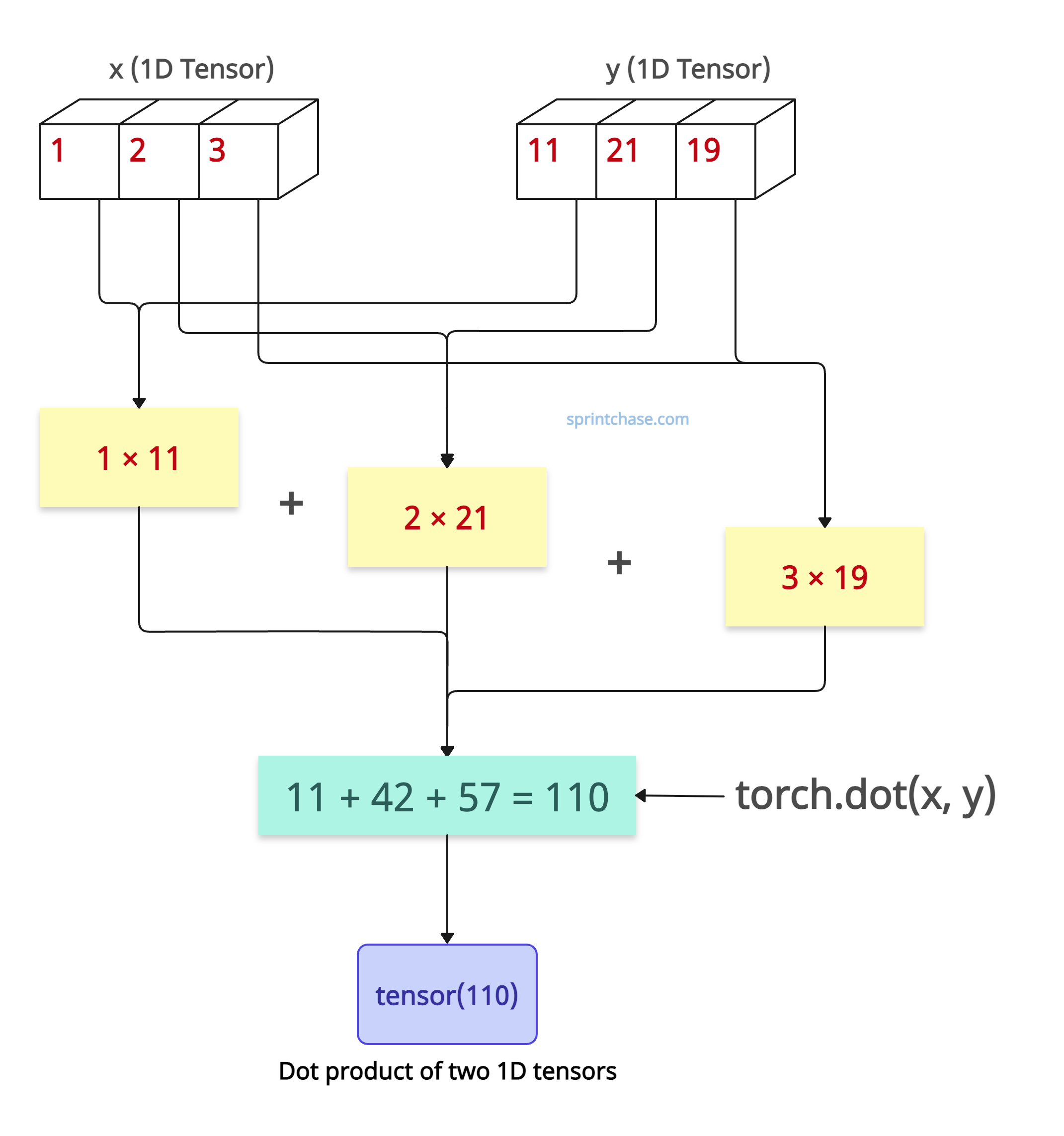
The torch.dot() is a fundamental PyTorch operation for computing the dot (inner) product of two 1D tensors of the same length. The output is always a scalar tensor.

The above figure shows how the .dot() method works.

This operation is highly efficient and supports both CPU and GPU execution. It internally dispatches BLAS or CUDA routines.

Make sure that both tensors reside on the same devices. For example, if you are executing on a CPU, both must be on a CPU. It should not be like one is in the CPU and another is in the GPU.

Both tensors must have the same data type (e.g., float32, int64).

The dot product operation fully supports autograd, enabling gradient flow through inner‑product operations.

Syntax

torch.dot(input, tensor, out=None) → Tensor

Parameters

Name	Value
input (Tensor)	It is an input 1D tensor.
tensor (Tensor)	Another 1D tensor of the same shape as the input 1D tensor.
out (Tensor, Optional)	It is a tensor to write the result into.

Basic Usage

import torch  

# Define 1D tensors  
x = torch.tensor([1, 2, 3])  
y = torch.tensor([11, 21, 19])  

# Calculate the dot product  
scalar_output = torch.dot(x, y)  # 1*11 + 2*21 + 3*19 = 110  

print(scalar_output)

# Output: tensor(110)

You can see that it multiplied each element of x by the corresponding element of y. Then, it summed up the products, resulting in an output of 110.

What if the tensor is 2D?

You wanted to perform the dot product on two tensors, but both are two-dimensional. How can you do that? In that case, we need to flatten them to 1D first.

import torch  

# 2D tensors
x = torch.randn(2, 3)
y = torch.randn(2, 3)

# Flattening to 1D tensors
x_1d = x.view(-1)
y_1d = y.view(-1)

# Calculate the dot product  
scalar_output = torch.dot(x_1d, y_1d)

print(scalar_output)

# Output: tensor(0.0467)

If you execute the above program multiple times, each time, it will return a different output because we are choosing random tensors for multiplication.

Mismatched lengths

What if the vectors you are working with have different lengths? If you go ahead with that, it will throw a RuntimeError saying that the “sizes do not match”.

To handle this RuntimeError, we can wrap our code with a try/except mechanism.

import torch  

# Mismatched length vectors
a = torch.tensor([1, 2])  
b = torch.tensor([3])  

try:  
    torch.dot(a, b)  # Raises RuntimeError  
except RuntimeError as e:  
    print(e)  # "sizes do not match"  


# Non-1D inputs  
matrix = torch.tensor([[1, 2], [3, 4]])  
try:  
    torch.dot(matrix, matrix)  # Raises RuntimeError  
except RuntimeError as e:  
    print(e)  # "1D tensors expected"  


# Output:

# inconsistent tensor size, expected tensor [2] and src [1] to have the same number of elements, 
# but got 2 and 1 elements respectively

# 1D tensors expected, but got 2D and 2D tensors

In the above code, we checked two different scenarios:

1. In the first scenario, we took two 1D vectors of different lengths. Since they have different sizes, we got an error saying ‘inconsistent tensor size’.
2. In the second scenario, we took 2D input tensors and, without flattening them, passed them directly to the tensor.dot() function. As a result, it throws an error saying it got 2D and 2D tensors instead of 1D tensors.

Ensure that both tensors have the same length and are both 1D tensors.

Calculating linear regression

If you have weights and features as input tensors, you can calculate a prediction as a weighted sum.

import torch  

weights = torch.tensor([0.5, -0.2, 1.3], requires_grad=True)  
features = torch.tensor([2.0, 3.5, 1.0])  

prediction = torch.dot(weights, features)  # Differentiable operation  

print(prediction)

# Output: tensor(1.6000, grad_fn=<DotBackward0>)

Cosine similarity

Let’s calculate the cosine of the angle between two vectors to measure their directional similarity, regardless of the magnitude.

import torch

def cosine_similarity(a, b):
    
    # 1. Normalize each vector to unit length
    a_norm = a / torch.norm(a)
    b_norm = b / torch.norm(b)
    
    # 2. Dot product of the normalized vectors = cos(θ)
    return torch.dot(a_norm, b_norm)

vec1 = torch.tensor([1.0, 2.0, 3.0])
vec2 = torch.tensor([4.0, 5.0, 6.0])

similarity = cosine_similarity(vec1, vec2)

print(similarity) 

# Output: tensor(0.9746)

Batched Inner Products

For multiple dot products at once, reshape and use matrix multiplication:

import torch

batch_a = torch.randn(32, 64)
batch_b = torch.randn(32, 64)

# element‑wise multiply, then sum across dim=1
dots = (batch_a * batch_b).sum(dim=1)  # shape (32,)

print(dots)

# Output: tensor([ 14.4743,  -7.5133,   4.0247,  -5.6994,  13.4800,   9.2407,  -2.5506,
        #   7.3114,   2.7754, -12.2593,   7.3131,   8.6266,  -8.3584, -18.2619,
        #   9.7819,  -6.1383,  -5.4524,  10.8361, -21.2875,   2.7174,   0.1096,
        # -10.9475,  15.2096,  -4.7224,   2.2955,  -9.6724,   2.4190,  -7.6380,
        # -18.4733,  -5.5328,  -3.4550,   0.1154])

If you’re working with multidimensional matrices, I recommend using torch.matmul() method or @ operator.

That’s all!