The torch.squeeze() and torch.unsqueeze() are utility methods in PyTorch that manipulate the dimension of the input tensor. It simplifies the tensor’s shape when it is required in specific operations.

The above figure conceptually and factually represents how squeeze and unsqueeze work in a PyTorch tensor. We transformed a 2D tensor into 3D by unsqueezing and a 3D tensor into 2D by squeezing.
torch.squeeze()
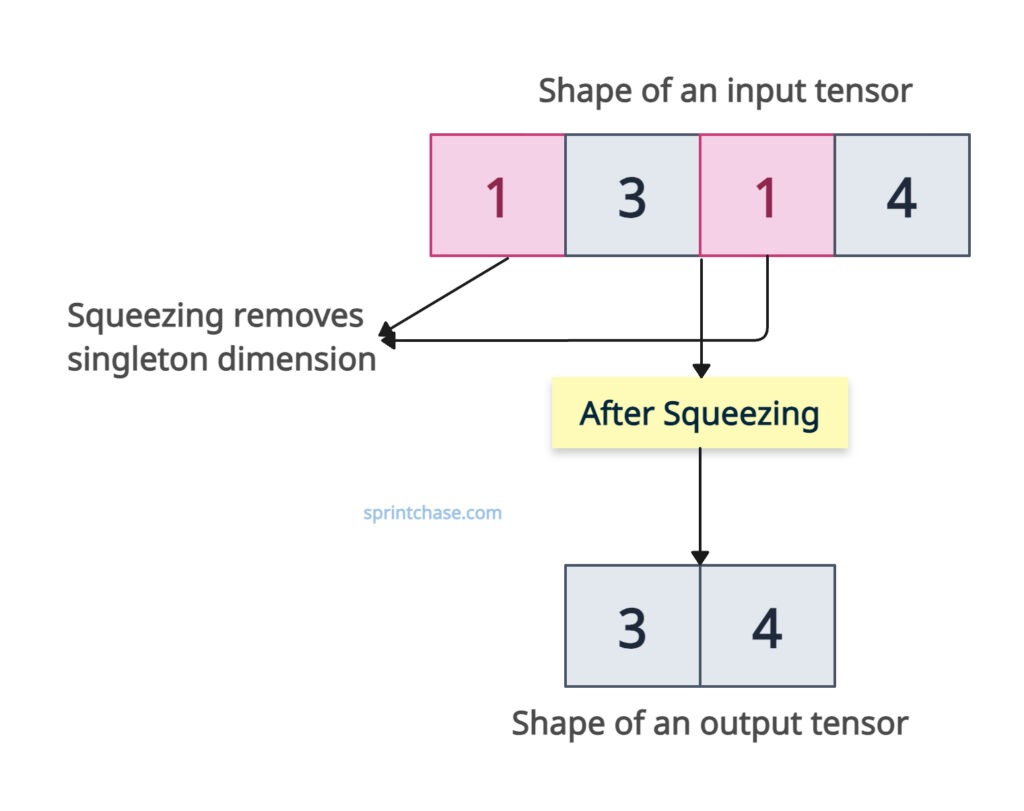
The torch.squeeze() method removes a dimension of size 1 (singleton dimensions) from the input tensor’s shape. So if a tensor has a shape like (1, 3, 1, 4), squeeze might remove those singleton dimensions, and the output shape would be (3, 4).
The output tensor shares storage with the input tensor, so modifying the contents of one will change the contents of the other. It returns a view when possible, avoiding unnecessary data copying and making it more efficient.
If a dimension is not of size 1 and is specified in dim, the output tensor is unchanged. This selective squeezing helps us to control which dimensions are removed.
Please note that the number of elements remains the same after squeezing; only the shape of the tensor changes.
Squeezing’s main use case is aligning tensor shapes for operations that rely on broadcasting, such as element-wise addition or matrix multiplication.
Syntax
torch.squeeze(input, dim=None)
Parameters
| Argument | Description |
| input (Tensor ) | It represents the input tensor that needs to be squeezed. |
| dim (int or tuple of ints, optional) | It defines an integer or a tuple of integers specifying the dimension to squeeze. If provided, only that dimension is squeezed if its size is 1. If not provided, all dimensions of size 1 are removed. |
Remove all singleton dimensions

Let’s define a tensor using torch.randn() and using the .squeeze() method, we will remove all the dimensions with size 1.
import torch tensor_with_singletons = torch.randn(1, 3, 1, 4, 1) print(tensor_with_singletons.shape) # Output: torch.Size([1, 3, 1, 4, 1]) removed_all_singletons = tensor_with_singletons.squeeze() print(removed_all_singletons.shape) # Output: torch.Size([3, 4])
The above code shows that we removed all the singletons from the input tensor, and the output tensor now has the shape of [3, 4].
Specifying a dimension

It provides an option to specify which dimension to squeeze. We can pass dim=1, which will squeeze dimension one and not touch any other dimension.
import torch
# Create a tensor with a singleton dimension
tensor = torch.randn(1, 3, 4)
print("Original shape:", tensor.shape)
# Output: Original shape: torch.Size([1, 3, 4])
# Squeeze dimension 0
squeezed = torch.squeeze(tensor, dim=0)
print("Squeezed shape:", squeezed.shape)
# Output: Squeezed shape: torch.Size([3, 4])
# Try squeezing dimension 1 (size 3, not 1)
squeezed_nothing = torch.squeeze(tensor, dim=1)
print(squeezed_nothing.shape)
# Output: torch.Size([1, 3, 4])
In the above code, we squeeze at dim=0, which removes a singleton dimension and changes the shape from (1, 3, 4) to (3, 4). In the next step, we squeeze at dim=1, which has no effect because the dimension’s size is 3, not 1, so the shape remains (1, 3, 4).
In-place modification
For in-place modification, you can use the tensor.squeeze_() method. It won’t return a new tensor. It will modify the original tensor. If you are looking for a new tensor, this is not the right approach.
import torch tensor = torch.randn(1, 5, 1) print(tensor.shape) # Output: [1, 5, 1] # In-place removal tensor.squeeze_() print(tensor.shape) # Output: torch.Size([5])
No singleton dimensions
What if the input tensor does not contain any singleton dimension? How to deal with that? Well, it will return the unchanged tensor. Meaning it will return the same input tensor as an output.
import torch tensor = torch.randn(2, 3) print(tensor.shape) # Output: torch.Size([2, 3]) no_change_tensor = tensor.squeeze() print(no_change_tensor.shape) # Output: torch.Size([2, 3])
The above output shows that the no_change_tensor is the same as the input tensor.
torch.unsqueeze()

The torch.unsqueeze() method returns a new tensor with a dimension of size 1 inserted at the specified position. It shares the same data as an input tensor. It helps align the shape of the tensor for broadcasting or batch processing.
For example, if an input tensor has a shape of (3, 4), using unsqueeze twice, the output tensor has a (1, 3, 1, 4) shape.
It does not modify the original tensor; it returns a new tensor with modified dimensions.
Syntax
torch.unsqueeze(input, dim)
Parameters
| Argument | Description |
| input (Tensor) | It represents an input tensor that will be modified. |
| dim (int) |
It defines an index at which we will add a singleton dimension. It must satisfy -input.dim() – 1<= dim <= input.dim(). For a tensor with d dimensions, dim can range from -d-1 to d. |
Unsqueezing a tensor
In the above section, we squeezed a tensor by removing one dimension. We will unsqueeze that tensor by adding a 1D at specified positions.
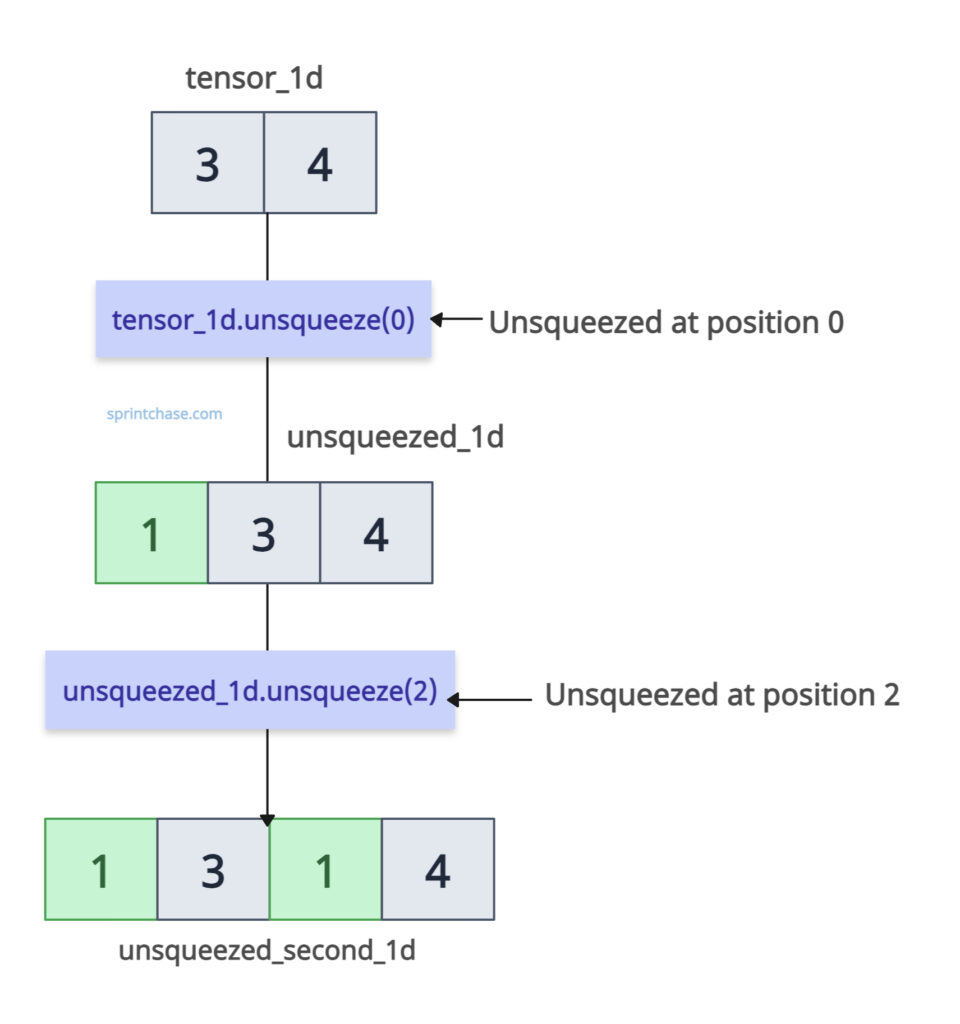
import torch tensor_1d = torch.randn(3, 4) print(tensor_1d.shape) # Output: torch.Size([3, 4]) # Adding a dimension at position 0 unsqueezed_1d = tensor_1d.unsqueeze(0) print(unsqueezed_1d.shape) # Output: torch.Size([1, 3, 4]) # Adding another dimension at position 2 unsqueezed_second_1d = unsqueezed_1d.unsqueeze(2) print(unsqueezed_second_1d.shape) # Output: torch.Size([1, 3, 1, 4])
Converting 1D vectors to 2D matrices
If a tensor is one-dimensional, you can call it a vector.
If a tensor is two-dimensional, you can call it a matrix.
Using unsqueezing, we can convert 1D to 2D by adding a new dimension.
There are two ways you can go from here:
- You can create a 2D tensor row-wise by passing unsqueeze(0).
- You can create a 2D tensor column-wise by passing unsqueeze(1).
Row-wise
import torch tensor_vec = torch.tensor([8, 12, 17]) print(tensor_vec.shape) # Output: torch.Size([3]) tensor_2d_row = tensor_vec.unsqueeze(0) print(tensor_2d_row) # Output: tensor([[ 8, 12, 17]]) print(tensor_2d_row.shape) # Output: torch.Size([1, 3])
Column-wise
import torch tensor_vec = torch.tensor([8, 12, 17]) tensor_2d_col = tensor_vec.unsqueeze(1) print(tensor_2d_col) # Output: # tensor([[ 8], # [12], # [17]]) print(tensor_2d_col.shape) # Output: torch.Size([3, 1])
Broadcasting alignment
As we already discussed, squeezing and unsqueezing become necessary to broadcast the tensor.
We can align tensors for arithmetic operations.
To perform a sum operation, both tensors should have the same shape. If not, we can unsqueeze them to make them the same and then execute the sum.
import torch tensor_1d = torch.tensor([1, 2, 3]) print(tensor_1d.shape) # Output: torch.Size([3]) tensor_2d = torch.tensor([[1, 2, 3], [4, 5, 6]]) print(tensor_2d.shape) # Output: torch.Size([2, 3]) # Unsqueeze to convert 1D tensor to 2D tensor converting_2d = tensor_1d.unsqueeze(0) print(converting_2d.shape) # Output: torch.Size([1, 3]) # Now we can add both tensors tensor_sum = tensor_2d + converting_2d print(tensor_sum) # Output: tensor([[2, 4, 6], # [5, 7, 9]])
In the above code, tensor_1d is one-dimensional. So, we will unsqueeze it to make it a 2d tensor and then perform a summation.
The output is without any error, so we successfully unsqueezed it.
That’s all!




