How to Check If a Tensor is Contiguous in PyTorch

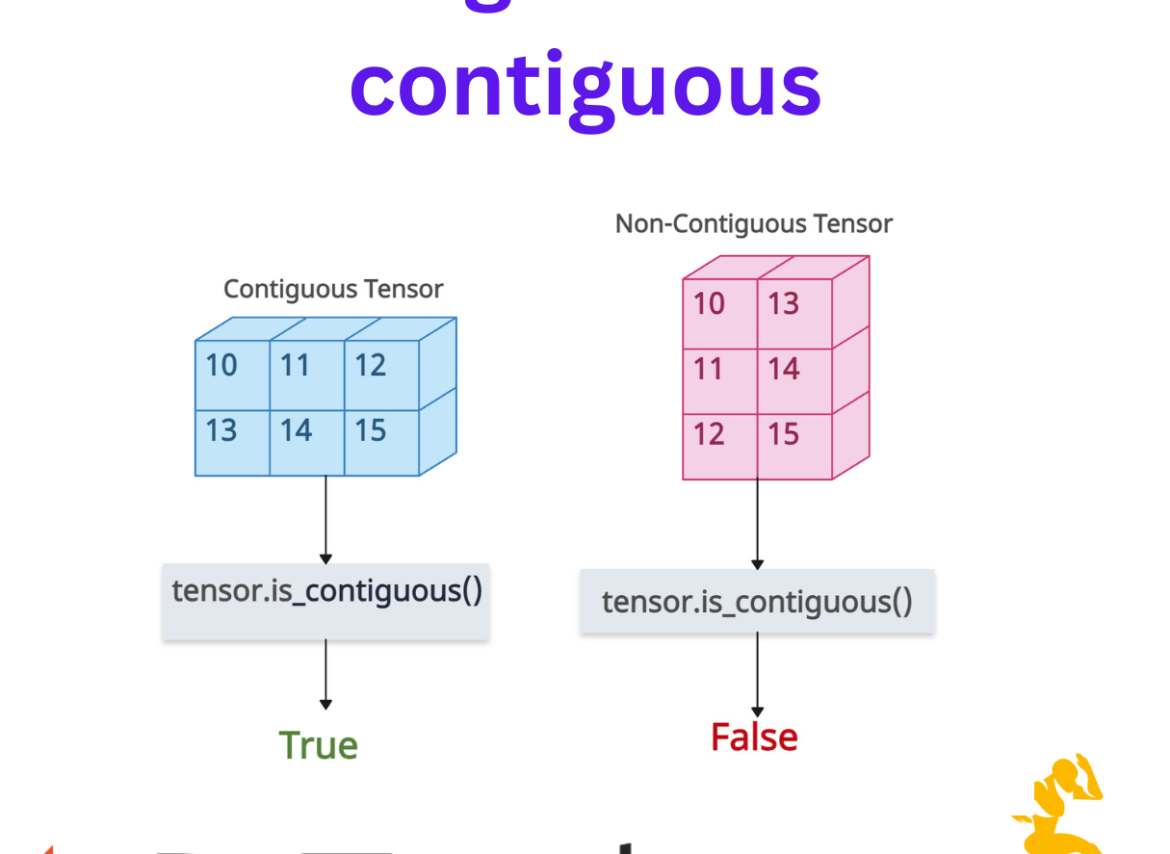
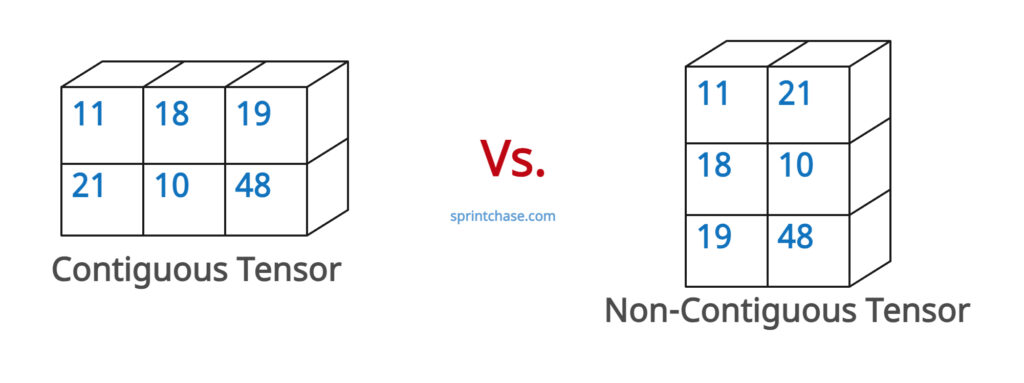
A contiguous tensor means a tensor whose elements are stored in memory with a stride for each dimension.

In simple words, how elements are laid out in a single, unbroken block (row-major order by default) without having any empty space between them. For example, if you have a 2D tensor, row after row, without any gaps.

A non-contiguous tensor means a tensor where the stride pattern doesn’t correspond to simple row-major (e.g., after a transpose, permute, slice with step, or expand).

Why does contiguity matter? Contiguity matters because some operations (like .view()) require the tensor to be contiguous in memory; otherwise, you must first call .contiguous() to get a copy that is laid out correctly.

To check if a tensor is contiguous in PyTorch, always use the is_contiguous() method. It returns True for a contiguous tensor and False otherwise.

If you create a new tensor and change its stride, it becomes a non-contiguous tensor.

A freshly created tensor is contiguous by default.

import torch

tor = torch.tensor([[11, 18, 19], [21, 10, 48]])

print(tor.is_contiguous())  

# Output: True

You can see that it is contiguous by default. What if we transpose it and then check its contiguity?

Transposing dimensions (e.g., transpose()) changes strides and often makes the tensor non-contiguous.

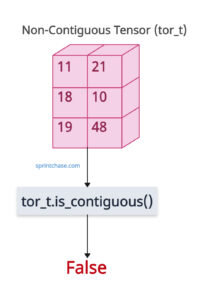
import torch

tor = torch.tensor([[11, 18, 19], [21, 10, 48]])

tor_t = tor.t()

print(tor_t.is_contiguous())  

# Output: False

As expected, it returns False.

Restoring contiguity

You can convert a non-contiguous tensor to a contiguous tensor using the .contiguous() method provided by PyTorch. It creates a contiguous copy of a non-contiguous tensor.

import torch

tensor_2d = torch.tensor([[19, 21], [18, 48]])

tensor_non_contig = tensor_2d.t()

print(tensor_non_contig.is_contiguous())
# Output: False

tensor_contig = tensor_non_contig.contiguous()

print(tensor_contig.is_contiguous())
# Output: True

Slicing

When you slice a tensor, you have to check whether it is sliced along rows or columns.

If you slice a tensor by rows, it preserves the contiguity because it does not change the strides.

import torch

tor = torch.tensor([[11, 18, 19], [21, 10, 48]])

sliced_by_row = tor[1:, :]

print(sliced_by_row.is_contiguous())  

# Output: True

If you slice a tensor by columns, it does not preserve the contiguity and changes the strides.

import torch

tor = torch.tensor([[11, 18, 19], [21, 10, 48]])

sliced_by_columns = tor[:, 1:]

print(sliced_by_columns.is_contiguous())  

# Output: False

Permuting dimensions

When you permute the dimensions, the tensor reorders the strides, which breaks the contiguity and makes it a non-contiguous tensor.

Let’s initialize a tensor using tensor.randn() method and then permute the dimensions.

import torch

tensor_3d = torch.randn(2, 3, 4)

print(tensor_3d.shape)
# Output: torch.Size([2, 3, 4])

tensor_permuted = tensor_3d.permute(2, 0, 1)

print(tensor_permuted.shape)
# Output: torch.Size([4, 2, 3])

print(tensor_permuted.is_contiguous())
# Output: False

You can see from the above output that arbitrary reordering of dimensions using the .permute() method almost always breaks the natural memory layout.

Expanding dimensions

If you expand the existing tensor’s dimension, you are essentially introducing “virtual” repetition, which leads to non-contiguity.

import torch

tensor_1d = torch.tensor([19, 21, 18])

print(tensor_1d.shape)
# Output: torch.Size([3])

tensor_expanded = tensor_1d.expand(2, 3)

print(tensor_expanded.shape)
# Output: torch.Size([2, 3])

print(tensor_expanded.is_contiguous())
# Output: False

Manually adjusting strides

If you try to adjust the strides of the existing tensor manually, you can use the as_strided() function, which results in a non-contiguous tensor.

import torch

tensor_1d = torch.tensor([19, 21, 18, 48])

print(tensor_1d.shape)
# Output: torch.Size([4])

tensor_strided = torch.as_strided(tensor_1d, size=(2, 2), stride=(1, 2))

print(tensor_strided.shape)
# Output: torch.Size([2, 2])

print(tensor_strided.is_contiguous())
# Output: False

That’s all!